Bitwise division

Posted on February 26, 2023 | Leave a comment

Integer division is expensive. Much more expensive than multiplication. Much, much more expensive than addition. If you’re trying to make some integer operations really fast it’s bad news if you need to do division.

A while ago, for a hobby project, I happened to be playing around with variable-length integer encodings. Where you store integers such that small ones take up less space than large ones. This is the kind of thing you want to be very fast indeed. At one point I ended up with this expression on a hot code path:

(63 - nlz) / 7

For everything else I could come up with fast ways of doing it using bitwise operations but this one place I ended up with division. And in this case not only is it expensive it’s overkill: the value we’re dividing by is a constant and in this case nlz is known to be between 0 and 63.

I thought: I’ll experiment a bit and see if I can’t come up with some bitwise operations that work just like dividing by 7 when the input is between 0 and 63. The one kind of division that is very cheap is by a power of 2, that’s just bit shifting. And it happens to be the case that 7 * 9 = 63, which is almost 64, a power of 2. Putting those together I got something I thought might do the trick:

$\frac{v}{7} = \frac{9 v}{9 \times 7} = \frac{9 v}{63} \approx \frac{9 v}{64}$

This you can compute with bitwise operations!

(9 * v) / 64
= (9 * v) >> 6
= (v + 8 * v) >> 6
= (v + (v << 3)) >> 6

Not bad! An expression that is purely bitwise operations but that computes almost division by 7. How “almost”? It turns out that this works for 0 to 6 but gives the wrong answer for 7: it yields 0 where it should be 1. Okay, it’s off by 1 — let’s try adding 1 then:

(v + (v << 3) + 1) >> 6

Now it’s correct from 0 to 13 but gives the wrong answer for 14: 1 where it should be 2. So let’s try adding 2 instead of 1. That makes it works for 0 to 20. If we keep increasing the fudge factor as long as we keep getting the right answer we end up with:

(v + (v << 3) + 9) >> 6

This computes v / 7 correctly for v from 0 to 69 which was what I needed originally. Actually I only needed up to 63.

Excellent! Problem solved! So let’s get back to varint encoding? Well, now I was on my way down the rabbit hole of bitwise division. What if it wasn’t 7 I needed to divide by, could I do something similar for other values? Where did the limit of 69 come from, and the fudge factor of 9?

Let’s generalize

A quick recap: because 7 * 9 = 64 - 1 we can implement v / 7 like this:

(9 * v + 9) / 64
= (v + (v << 3) + 9) >> 6

for v between 0 and 69.

Put more abstractly: given a divisor d, which happened to be 7, we found a power of 2, 64 = 2⁶, such that

$d m = 2^n - 1$

for a multiplier value m which in this case was 9.

Using this together with a fudge factor a which also turned out to be 9, we were able to replace division by d with

(m * v + a) >> n

which gives the correct result for values between 0 and some limit L, where L in this case was 69.

Now, what if I wanted to divide by some other value than 7? Let’s say 43? Then we have to find an n such that

$43 m = 2^n - 1$

for some m. That just means an n such that 43 is a factor in 2ⁿ-1. I’ve put a table of the prime factors of 2ⁿ-1s at the bottom. There is one: 2¹⁴-1.

$43 \times 381 = 2^{14} - 1$

So you can replace v / 43 with

(381 * v + a) >> 14

for some choice of a, and then it will be correct for values up to some limit L. What should a be and what will that make L? Well, let’s try to derive them. Let’s start with a. (And just skip the derivations if this kind of stuff bores you).

One thing that definitely must hold is that if you bitwise-divide 0 by d the result must be 0:

(m * 0 + a) >> n = 0

$\left\lfloor{\frac{0 m + a}{2^n}}\right\rfloor = 0$

$\left\lfloor{\frac{a}{2^n}}\right\rfloor = 0$

$0 \le a < 2^n$

So we know that definitely the fudge factor must be non-negative. Similarly if you bitwise-divide d-1 by d the result must also be 0; that gives us:

(m * (d - 1) + a) >> n = 0

$\left\lfloor{\frac{(d - 1)m + a}{2^n}}\right\rfloor = 0$

$0 \le (d - 1)m + a < 2^n$

$0 \le md - m + a < 2^n$

$0 \le 2^n - 1 - m + a < 2^n$

$-1 - m + a < 0$

$a < m + 1$

Putting those two together we get that

$0 \le a \le m$

But which a to choose? There we can use the fact that bitwise division increases more slowly then real division so when it gets the answer wrong, it’ll be because it returns too small a value. So we want a to be the largest allowed value: m.

Next, let’s derive L. Or, let’s derive L+1, the first value where bitwise division yields the wrong result. Since bitwise division grows more slowly than division that will be at some multiple of d, k d, where it yields a value less than the true result: k – 1.

(m * k * d + m) >> n = k - 1

$\left\lfloor\frac{m k d + m}{2^n}\right\rfloor = k - 1$

$2^n(k-1) \le m k d + m < 2^nk$

$2^n(k-1) \le (2^n-1)k + m < 2^nk$

$2^n(k-1) \le 2^nk - k + m < 2^nk$

$-2^n \le m - k < 0$

$m < k$

The smallest k which yields a wrong result is hence the first value greater than m: m + 1 so that makes L:

L + 1 = k * d
L + 1 = (m + 1) * d
L = (m + 1) * d - 1

Just to verify let’s try the example from before: 7

L = (9 + 1) * 7 - 1
= 69

Another useful way to write this is

L = (m + 1) * d - 1
= (m * d) + d - 1
= 2ⁿ - 1 + d - 1
= 2ⁿ + (d - 2)

This means that for any d > 2 L is at least 2ⁿ. That gives a nice rule of thumb: the bitwise division by 43 above holds for all values up to 2¹⁴. And then a bit more.

Can you always find a value of n that lets you do bitwise division? In theory probably yes, I’m not good enough at number theory to say definitively. But since in practice we’re working with finite numbers you usually want n to be less than 32 and then the answer, at least initially, is no. Here are some values that you can’t bitwise divide with an n at most 32:

37, 53, 59, 61, 67, 71, 79, 83, 97

Does that mean that if we end up having to divide by 37 there is no way to express that as a bitwise operation? No. This exact approach doesn’t work but there are others. For instance, so far we’ve only looked at dm = 2ⁿ-1. There’s also dm = 2ⁿ+1 — maybe we can use that when 2ⁿ-1 doesn’t work? (Spoiler: yes we can, not always but often). What about dm = 2ⁿ-2, might that be useful somehow? There’s more fun to be had with this. But that’s for another post.

Appendix

Prime factors of 2ⁿ – 1 for n up to 32 (Mersenne primes marked in bold).

n	prime factors of 2ⁿ – 1
2	3
3	7
4	3, 5
5	31
6	3, 3, 7
7	127
8	3, 5, 17
9	7, 73
10	3, 11, 31
11	23, 89
12	3, 3, 5, 7, 13
13	8191
14	3, 43, 127
15	7, 31, 151
16	3, 5, 17, 257
17	131071
18	3, 3, 3, 7, 19, 73
19	524287
20	3, 5, 5, 11, 31, 41
21	7, 7, 127, 337
22	3, 23, 89, 683
23	47, 178481
24	3, 3, 5, 7, 13, 17, 241
25	31, 601, 1801
26	3, 2731, 8191
27	7, 73, 262657
28	3, 5, 29, 43, 113, 127
29	233, 1103, 2089
30	3, 3, 7, 11, 31, 151, 331
31	2147483647
32	3, 5, 17, 257, 65537

Reverse index: for a prime, which 2ⁿ-1s is it a factor of:

p	n where p is a prime factor of 2ⁿ-1
3	2, 4, 6, 6, 8, 10, 12, 12, 14, 16, 18, 18, 18, 20, 22, 24, 24, 26, 28, 30, 30, 32
5	4, 8, 12, 16, 20, 20, 24, 28, 32
7	3, 6, 9, 12, 15, 18, 21, 21, 24, 27, 30
11	10, 20, 30
13	12, 24
17	8, 16, 24, 32
19	18
23	11, 22
29	28
31	5, 10, 15, 20, 25, 30
41	20
43	14, 28
47	23
73	9, 18, 27
89	11, 22
113	28
127	7, 14, 21, 28
151	15, 30
233	29
241	24
257	16, 32
331	30
337	21
601	25
683	22
1103	29
1801	25
2089	29
2731	26
8191	13, 26
65537	32
131071	17
178481	23
262657	27
524287	19
2147483647	31

→ Leave a comment

Posted in Uncategorized

World history is off by one

Posted on December 16, 2019 | Leave a comment

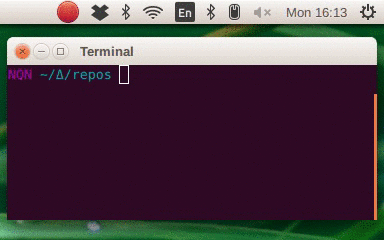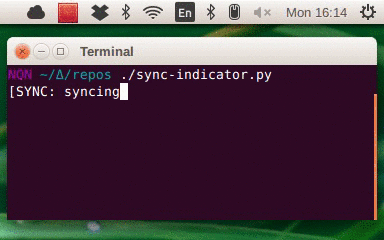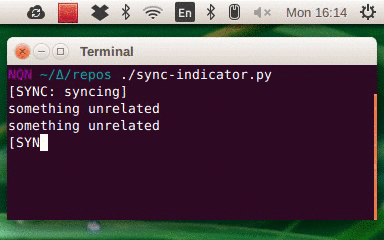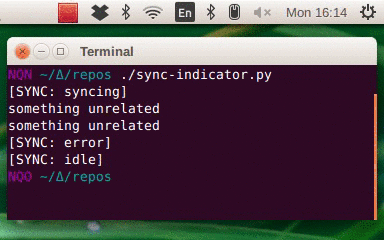
New years eve 2019 is only a few weeks away. The end of the decade. The last day of the 2010, then the first of the 2020s.

Or is it?

This post is about calendars and how we assign numbers to years. I’ll explain why, if you look closely at them, years like 120 BC, AD 14, and 2019, aren’t as straightforward as you might think. Then I’ll describe the off-by-one error that has led to all this confusion rippling down through the centuries: the year that should be year 0 but isn’t. Finally I’ll suggest a different way of counting years that makes most of this confusion go away.

Let’s start off with a classic exchange from Seinfeld (S8E20, “The Millennium”):

Jerry: By the way, Newman, I’m just curious, when you booked the hotel, did you book it for the millennium new year?

Newman: As a matter of fact, I did.

Jerry: Oh that’s interesting, because, as everyone knows since there was no year zero, the millennium doesn’t begin until 2001, which would make your party one year late, and thus, quite lame. Oooooh.

Newman: *squawnk*

Wait, what? I’m old enough to remember that the big millennium new year was on the evening of December 31, 1999. Wasn’t it? I’m pretty sure it was.

What’s in a millennium?

Let’s say Jerry is right – and in fact he is – that this millennium only started in 2001. What does that make the year 2000? Which century is it in? Is it in the twentieth or twenty-first century? The twentieth century is the 1900s right so surely it’s not in that? If the 1900s means anything it must be years that start with 19. So it must be the twenty-first century? But then that would mean that on new years eve of 1999 we went from the twentieth to the twenty-first century. But since we’re assuming Jerry is right we then had to wait until 2001 to go from the second to the third millennium. That sounds all wrong though, centuries and millenniums must match up, and decades too. Speaking of that, which decade is 2000 in? Surely it’s not in the 1990’s right, surely. Right?

Okay so you may suspect that I’m deliberately making this sound more confusing that it is, and I am; sorry about that. It does actually all make sense – sort of – but is still a little unexpected.

The core question is: what is a millennium, a century, a decade? The answer is that any period of 1000 years is a millennium, any period of 100 years is a century and any period of 10 years is a decade. So the years 1990-1999 is a decade but so is 1945-1954. Similarly the years 1000-1999 is a millennium but so is 454-1453. None of these terms have anything to do with where on the time scale they occur, they’re just periods of a particular number of years.

This means that the first millennium is the first sequence of 1000 years, wherever they fall on the timeline. As Jerry says, because there is no year 0 the first year is AD 1. A thousand years later is AD 1000 so that’s the first millennium: AD 1 up to and including AD 1000. The first year of the second millennium is AD 1001 and the last is AD 2000. So we did indeed only enter the new millennium in 2001.

It works the same way for centuries and decades. The first century was AD 1 to AD 100, the second was AD 101 to AD 200, and so. Following it all the way up to our time you get that the twentieth century covers 1901 to 2000. So I was really lying before when I said that the twentieth century was the same as the 1900s. Each have one year that is not in the other: the 1900s have 1900 which is in nineteenth century, and the twentieth century has 2000 which is not in the 1900s.

Similarly, to come back to this coming new years eve: the 2010s do indeed end when we leave 2019 – but the second decade of our century actually keeps going for another year until the end of 2020. So it’s the end of the decade but it also isn’t because “this decade” has two possible meanings.

Jesus!

Let’s take a quick detour and talk about what AD means. We usually leave out the “AD” when we talk about modern years, nobody calls it 2019 AD, but the AD is there implicitly. And it’s what all this confusion springs from.

AD means Anno Domini, literally “in the year of the lord”, the lord in question being Jesus. It’s really an exercise in religious history, one that goes back to the darkest middle ages, so maybe it’s not surprising if modern pedants like me stumble over the mathematics of it.

Already at this point, before we’ve even gone into where AD comes from, things become murky. Consider this. If 2019 means “2019 years since the birth of Jesus”, and we assume Jesus was born in December, how old would he turn in December 2019? Presumably 2019 should be the year he turns 2019 right? But if he was born in AD 1 his 1-year birthday would have been in AD 2 and then 2019 is the year of his 2018’th birthday. He would have had to be born in 1 BC for the years to match up. But 1 BC is expressly not a “year of the lord”. Either the years don’t match up or Jesus – the actual lord – lived, at least briefly, in a year that wasn’t “of the lord”.

The first person to count years Anno Domini was a monk, Dionysius the Humble. (Side note: imagine a person so humble that he stands out among monks as the humble one). Back then, in the early 500s, the most common way to indicate a year was by who was roman consul that year. The year Dionysius invented AD would have been known to him and everyone else at the time as “the year of the consulship of Probus Junior”. But he was working on a table of when Easter would fall for the following century and when you’re dealing with 50 or 100 years into the future how do you denote years? You don’t know who will be consul. Dionysius decided to instead count years “since the incarnation of our Lord Jesus Christ”. By this scheme his present year was 525. How did he decide that at that moment it had been 525 years since the “incarnation”? We don’t really know, though some people have theories.

Note that this means that when historians argue that Jesus was more likely born between 6 BC and 4 BC they’re not disagreeing with the bible, the bible doesn’t specify a particular year. It was Dionysius, much later, who decided the year so he’s the one they’re disagreeing with.

In any case Dionysius wasn’t clear in his writing on what “since the incarnation” actually means so we don’t know if he believed Jesus was born in 1 BC or AD 1. The question from before about Jesus’ age doesn’t have a clear answer, at least not based on how years are counted. Most assume he meant 1 BC so the years and Jesus’ birthdays match up but we’re really not sure.

Year Zero

Now let’s backtrack a little to where we were before this little historical diversion: the off-by-one error in how we count years. The year numbers (1900s) and the ordinals (twentieth century) are misaligned.

It actually gets worse when you bring BC into it.

Here’s a little quiz. Take a moment to figure them out but don’t feel bad if you give up, they’re meant to be a little tricky. Also don’t worry about dates, assume that events all happened on the same calendar date.

The Napoleonic wars started in 1803 and ended in 1815. How many years was this?
Johann Sebastian Bach was born in 1685. Was that towards the beginning or the end of the 1600s? He died in 1750. How many years did he live?
Julius Caesar was in a relationship with Cleopatra. He was born in 100 BC, she in 69 BC. What was their age difference?
Mithridates the Great was born in 120 BC. Was that towards the beginning or the end of the 100s BC? He died in 63 BC. How many years did he live?
Phraates V ruled Persia from 4 BC to AD 2. How many years did he rule?

Notice how the questions are basically the same but they get harder? I’m the one who made them up and I struggled to solve the last three ones myself, or at least struggled to convince myself that my answers were correct. But let’s go through the answers.

The Napoleonic wars lasted 1815 – 1803 = 12 years.
The year Bach was born, 1685, is towards the end of the 1600s and he lived 65 years: 15 years until 1700 and 50 years after, 65 in total.
The age difference between Caesar and Cleopatra was 31 years because time counts backwards BC. 31 years on from 100 BC is 69 BC.
Mithridates was born towards the end of the 100s BC. Again, in BC the years count backwards so 120 BC means there’s 20 years left of that century, not that 20 years have passed like it would in AD. He lived 57 years: 20 years until 100 BC and then, again because time counts backwards in BC, 37 years until 63 BC.
Phraates ruled for 5 years. You’d think it should be 6: 4 years BC and 2 years AD, 6 in total – but there is no year 0, we skip directly from 1 BC to AD 1, so it’s really 5.

This highlights two issues with how we count years: it’s easy to work with modern years – we do it all the time – but everything gets turned upside down when you go to BC. You have to fight your normal understanding of what a year means – for instance the 20s of a century is now in the end, not the beginning. And you have to watch out especially for the missing year between 1 BC and AD 1.

There are models like astronomical time that insert a year 0 – or rather it renames 1 BC to 0 – and that helps a lot. But I don’t find it intuitive to work with negative years. For instance, I still have to turn off my normal intuition to get that -120 is before -115, not after.

I’m interested in ancient history and so I’ve stubbed my toe on this over and over again. I’ve also given some thought to what a more intuitive system might look like. What I’ve come up with, as a minimum, is: you would want to redefine BC 1 to be 0 AD. You would want years to always move forward; it’s more intuitive for the years’ names to move the same way as time: always forward. Finally you would want the years AD to stay unchanged since those are the ones we use every day, there’s no way to change those.

How about this?

Here is a system that has those properties.

Like in astronomy you redefine BC 1 to be 0 AD. Other than that we leave AD unchanged. In BC you reverse how you count the years but only within each century. So the years count up both during BC and AD but the centuries BC still count backwards. Finally, to distinguish it from what we currently do, rather than write BC after or AD before you would write a B or A between the centuries and the years. This also makes it clear that the centuries and years within them are treated differently, sort of how we usually separate hours and minutes with a colon: 7:45 rather than 745.

What does that look like? Here are some examples:

525 AD is unchanged but can be written as 5A25 if you want to be really explicit.
BC 1 is year zero AD and is written as 0 or, again if you want to be really explicit, 0A00.
BC 2 is the last year of the first century BC so that’s 0B99. Since we’re always counting forwards the last year of any century is 99, like centuries AD.
BC 3 is the year before 0B99 so 0B98. When going backwards in time we count the years backwards so the year before is one less.
BC 34 is 0B67 because it’s 33 years before the end of the first century BC. Just like 1967 is 33 years before 2000.
BC 134 is 1B67, just like BC 34 is 0B67. Only the years within the centuries are changed, the centuries stay the same (with a single exception).

There’s a simple general rule for converting the doesn’t require you to think, I’ll get to that in a second. First I’ll illustrate that this is indeed more intuitive by revisiting some questions from before but now written with this new system:

Julius Caesar was in a relationship with Cleopatra. He was born in 0B01, she in 0B32. What was their age difference?
Mithridates the Great was born in 1B81. Was that towards the beginning or the end of the 1B00s? He died in 0B38. How many years did he live?
Phraates V ruled Persia from 0B97 to 2. How many years did he rule?

I would suggest that it’s now a lot closer to how you normally think about years. Also, the ADs are no longer off by one: the first century starts in year 0 and runs 100 years, to year 99. The twentieth starts in 1900 making the millennium new year 1999. If only they’d used this system Newman’s party wouldn’t have been late, and thus, not lame.

The numbers are written differently, at least in BC where they actually are different, so it’s clear which system is being used. Converting from BC is straightforward.

Any year BC that ends in 01 becomes year zero in the next century. For instance, 201 BC (the year the Second Punic War ended) becomes 1B00 and 1001 BC (the year Zhou Mu Wang becomes king) becomes 9B00.
Any other year you keep the century and subtract the year from 101. For instance for 183 BC (the year Scipio Africanus died), the century stays 1 and the year is 101 – 83 = 18. So that’s 1B18.

(Technically you don’t need the first rule because when the year is 01, 101 – 01 = 100 which you can interpret as adding one to the century and setting the year to 00.)

It’s maybe a little cumbersome for the person writing if they’re used to BC/AD but it’s the same kind of operation you already need to do to understand years BC in the first place. And I would suggest that the result is easier for the person reading and that hopefully more people read than write a given text. It’s the same kind of operation to go back to BC though I’ll leave that as an exercise for the reader.

A small but relevant point is: how do you pronounce these? I would suggest still saying BC and AD but between the century and year rather than after the whole number. So where you would say “one eighty-three b-c” for 183 BC, with the new system you would say “one b-c eighteen” for the equivalent year 1B18. For the first century BC, “thirty-four b-c” for 34 BC becomes “zero b-c sixty-seven” for the equivalent 0B67.

That’s it. I’m curious what anyone else thinks. If one day there was an opportunity to change how years are written – like there was for measurements during the French revolution – would this be a sensible model to switch to? If not, is there another model that’s better?

→ Leave a comment

Posted in Uncategorized

More Than Voronoi

Posted on August 11, 2018 | Leave a comment

This post is about a generalization of Voronoi diagram that I played around with. It’s probably not that useful but it’s a little fun math with an absolute ton of colorful diagrams.

It occurred to me a while ago that there was a generalization of Voronoi diagrams that maybe could be useful to something I was working on. As you know, a Voronoi diagram divides the plane into regions based on a set of points. Given the points, p₀, p₁, …, p_n, the region corresponding to p_i is the set of points that are closer to p_i than any of the other p_j. Here is an example of a run-of-the mill, standard, plain vanilla, Voronoi diagram:

This diagram determines which points are closer using normal, cartesian, distance but Voronoi diagrams also make sense for other kinds of distance, for instance Manhattan distance:

The generalization that occurred to me was: if a region in a plain Voronoi diagram is defined by the one point it is closest to, what if you defined a diagram where regions are based on the two closest points? That is, for each pair of points, p_i and p_j, there would be a region made up of points where the closest point is p_i and the second-closest is p_j. What would that look like, I wondered. I searched around and it’s definitely a thing, it’s called a higher-order Voronoi diagram, but I couldn’t find any actual diagrams.

There may be some established terminology around this but I ended up using my own names: I would call what I just described a Voronoi² diagram, and a plain one would be a Voronoi¹. (From here on I’ll call the region around p_i in the Voronoi¹ diagram V(p_i), and the region around p_i and p_j in the Voronoi² diagram I’ll call V(p_i, p_j)).

You can kind of guess just from the definition that a Voronoi² would look similar to the corresponding Voronoi¹ just more subdivided. For any given p_i, the point’s region in the Voronoi¹ diagram, V(p_i), is the set of point closest to p_i. Well for any point in that set they will have some other point p_j as their second-closest, and so if you take the union over all p_j of V(p_i, p_j) that gives you V(p_i). So the regions in a Voronoi² diagram are basically fragments of regions of the Voronoi¹.

Below is the same diagram as before, for comparison, and the Voronoi² diagram.

As you can see, that is exactly what the Voronoi² diagram looks like: each Voronoi¹ region has been subdivided into sub-regions, one for each of its neighboring points. You can do the same thing for the Manhattan diagrams,

Now we’ve defined Voronoi¹ and Voronoi² but why stop there when we could keep going and define Voronoi³. This would be, you’ve probably already guessed it, a diagram with a region for each choice of p_i, p_j, and p_k, that is made up of the points that have p_i as their closest point, p_j as their second-closest, and p_k as their third-closest. Let’s call such a region V(p_i, p_j, p_k). As I’m sure you’ve already guessed the Voronoi³ regions are further subdivisions of the Voronoi² regions:

And the Manhattan version,

The images are becoming smaller but you can click them to see larger versions.

From here you can just keep going: Voronoi⁴, Voronoi⁵, Voronoi⁶, and so on and so on. Which of course I did, what did you expect? Here are Voronoi¹-Voronoi⁸ with cartesian distance,

and the same with Manhattan distance

Except… I lied before when I said you could just keep going. In this example there are 8 points so the Voronoiⁿ diagrams are only well-defined for n up to 8 – that’s why there’s 8 diagrams above. And indeed if you look closely diagram 7 and 8 are actually the same – because once you’ve picked 7 points there is no choice for the last point, there is only the 8th left, so the diagrams end up looking exactly the same.

So is that it – is that all the colorful diagrams we get? Well, there is just one last tweak we can make to get a different kind of diagram.

The thing is, in the definition of Voronoi² we said that V(p_i, p_j) was the points where p_i is the closest point and p_j is the second-closest. That is, the order of p_i and p_j is significant. An alternative definition we could use would be one where we don’t consider the order, where the region doesn’t care whether it’s p_i closest and p_j second-closest, or p_j closest and p_i second-closest. I’ll call this V_u(p_i, p_j) (the u is for unordered).

You’ll notice right away that by this definition V_u(p_i, p_j)=V_u(p_j, p_i) so there’s a lot fewer regions. Here’s an example of a Voronoi_u¹ (which is the same as the Voronoi¹) and Voronoi_u² diagram,

With these unordered diagrams it can be a little trickier to figure out which two points a region actually corresponds to, especially in cases where the points in question are far away from the region. The trick you can use in this case is that for a given region is in the Voronoi_u², if you look at the same place in the Voronoi¹ there will be a dividing line that goes across where the region is in the Voronoi_u², from one corner of the region to another. The two points on either side of the Voronoi¹ will be the one the region corresponds to.

The same things works, as always, with Manhattan distance:

An interesting thing happens if we plot all the Voronoi_uⁿ all the way up to 8:

The number of regions stays about the same and when we get to Voronoi_u⁷ and Voronoi_u⁸ they actually become simpler. This is because at that point the set of points for a given region includes almost all the points so the determining factor becomes which are the few points that aren’t in the set – and at 7 and 8 there’s 1 and 0 left respectively. So whereas Voronoi⁸ was useless because it’s the same as Voronoi⁷, here it’s useless because there’s only one region that contains all the points.

Is this construction at all useful? I’m not sure, I imagine it could be but I don’t have any particular use for them myself. Really I was just curious what it would look like.

I’ll leave you with a last set of diagrams, Voronoi_u¹ to Voronoi_u⁸ for Manhattan distance.

→ Leave a comment

Posted in Uncategorized

Stdout is a dead end

Posted on December 18, 2015 | Leave a comment

I haven’t written much about it on this blog but the project I’ve been working on full time for the last two years is a new kind of terminal, chorus. Current terminals are a relic of the past and chorus is my take on a modern replacement.

I’ve created a blog specifically about chorus, the chorus console blog. There I’ll be writing about the approach I’m taking and my thoughts about what terminals are and where they should be moving. The title of this post itself hints at where I see them evolving. But you can read more about that in the introductory post.

→ Leave a comment

Posted in Uncategorized

A simple way to pre-scramble a sequence

Posted on November 26, 2015 | 2 Comments

I have this problem where I need to try something a number of times, maybe 64 times, and each time with a different small seed, say a value between 0 and 1024. I’d like the seeds to be reasonably scrambled and I don’t want to see the same one more than once. I also need the same order every time, that’s what I mean by pre-scrambling – the scrambling isn’t dynamic, it’s hardcoded. How do I do this in a simple way without resorting to say just hard coding a list of numbers?

What I’d really like to do is use something like a random number generator but with pre-determined set parameters that I know will generate the numbers I want. The xorshift generator seems like a good candidate because it’s really simple but the quality is decent. It requires 4 parameters, x, y, z, and w, and then you can generate a sequence of values in the following way, where limit is the size of the set you want to generate:

t = x ^ (x << 11) & 0xFFFFFFFF
x = y
y = z
z = w
w = (w ^ (w >> 19) ^ t ^ (t >> 8)) & 0xFFFFFFFF
return w % limit

This is what I’d like to use — I just need some parameters. And it turns out that there are parameters that will make it behave like I want. Here’s an example,

0x31f12daf 0x6dd97342 0xda4daacd 0x41235c71: 85/256 85 (33.2% 1x)

This means: with these parameters x y z w and a limit of 256 you get 85 different values (that’s the 85 in “85/256”) if you execute the xorshift code 85 times (that’s the second 85), which means that you’re covering 33.2% of the possible values and executing the loop 1x per unique generated value. Here are some seeds for different limits that are powers of 2, that generate a pretty big set of unique values,

0x2735e8f4 0x9fcb0c3e 0xd0c18064 0x0f6b0093: 26/32 26 (81.2% 1x)
0x1ff079d6 0x54248059 0xc968e911 0x38c15c75: 39/64 39 (60.9% 1x)
0xf8efc789 0x88a40b37 0x86f01aa6 0x15384f52: 59/128 59 (46.1% 1x)
0x31f12daf 0x6dd97342 0xda4daacd 0x41235c71: 85/256 85 (33.2% 1x)
0xfd8193d0 0xc8b69d8f 0xa42b9d1c 0x7e69d727: 133/512 133 (26% 1x)
0x4617b049 0xf7a49270 0xa88b568c 0x32dff77c: 174/1024 174 (17% 1x)

As an example of how to use one of these, here’s how you’d use the first line, the one that generates values with a limit of 32, in python:

def generate():
  x = 0x2735e8f4
  y = 0x9fcb0c3e
  z = 0xd0c18064
  w = 0x0f6b0093
  for i in range(0, 26):
    t = (x ^ (x << 11)) & 0xFFFFFFFF
    x = y
    y = z
    z = w
    w = (w ^ (w >> 19) ^ t ^ (t >> 8)) & 0xFFFFFFFF
    yield w % 32

print list(generate())

This prints

[2, 18, 9, 30, 12, 0, 19, 17, 7, 5, 14, 16, 6, 24, 15, 4, 3,
31, 10, 29, 8, 23, 11, 22, 1, 26]

which, and you can check if you want, are 26 different values between 0 and 32.

If you can tolerate some duplicates you can get better coverage. If you can only tolerate a few, say about one duplicate in 16 values, you can get,

0xf852d2f8 0xaf137287 0x6a0d4795 0x326c8a41: 28/32 29 (87.5% 1x)
0xa8683488 0x361c1383 0xbc95298a 0xe4c57646: 46/64 49 (71.9% 1.1x)
0xca30a753 0x317aa350 0x1bc8bee2 0xce4830bf: 79/128 87 (61.7% 1.1x)
0xe079cdb3 0x7cb29574 0x45eebac8 0xeb8dcefc: 132/256 147 (51.6% 1.1x)
0xf41e4441 0x3345d823 0x608ff840 0x554f5cdd: 238/512 269 (46.5% 1.1x)
0x201ceef2 0x7f49ce17 0x0bd10615 0x139bfa7b: 423/1024 485 (41.3% 1.1x)

So for example in the 256 case, if you generate 147 values with the given seed you’ll hit 132 different values between 0 and 256, and the rest will be duplicates. That’s a lot better coverage than the 85 you could hit if you didn’t allow them.

If you can tolerate even more duplicates, say you don’t mind hitting roughly one on average per unique value, you can get close to full coverage

0xa9bb0026 0xe0178ff2 0x443fd052 0x9fe0d459: 32/32 41 (100% 1.3x)
0x4c19f4c7 0x1d253873 0x5c1f6f17 0x812944fc: 64/64 106 (100% 1.7x)
0x854fbffe 0x5aa965d5 0x06ff8c3e 0xd5057351: 127/128 252 (99.2% 2x)
0xeb03a458 0x26ae990e 0x6227aaee 0x192b3cb7: 242/256 496 (94.5% 2x)
0x97bbc402 0x20470416 0x09ce179b 0xbf276b7d: 469/512 980 (91.6% 2.1x)
0x6d36254c 0x19c5f46a 0x1614da1a 0xcfadbfc8: 915/1024 1939 (89.4% 2.1x)

As an example, running the same python code from above but now with parameters from this set you get,

[19, 27, 10, 12, 18, 16, 13, 15, 24, 4, 23, 11, 28, 30, 26,
19, 24, 1, 12, 15, 29, 2, 19, 8, 9, 20, 6, 5, 17, 3, 14, 31,
22, 25, 18, 27, 8, 20, 0, 7, 21]

In this list of length 41 all numbers between 0 and 31 occur, but 8, 12, 15, 18, 20, 24, and 27 are there twice and 19 is there three times.

Finally, if you don’t care how many times you try as long as you generate all the numbers that’s possible too. At this point you probably want to keep track of which value you’ve seen, maybe with a bit vector, and just filter the raw values you generate.

0xa9bb0026 0xe0178ff2 0x443fd052 0x9fe0d459: 32/32 41 (100% 1.3x)
0x4c19f4c7 0x1d253873 0x5c1f6f17 0x812944fc: 64/64 106 (100% 1.7x)
0xf3bd4634 0xb1442411 0xd536236f 0x3beae2fb: 128/128 291 (100% 2.3x)
0x1c608f31 0x34e54bbd 0xa799c7a8 0x78af6664: 256/256 729 (100% 2.8x)
0x10bace53 0x88bc0781 0xd815fe20 0xc77bcbec: 512/512 1786 (100% 3.5x)
0xb6c93670 0xb89f9de6 0x3ba3713c 0x78bcabc7: 1024/1024 4341 (100% 4.2x)

If you look closely you’ll notice that the parameters are the same as before for some limits, that’s because we already had perfect coverage before so there’s nothing to improve. And as the set grows you can see that the number of times you have to try grows, so at 1024 you need to loop 4341 times before you’ve seen all values. And note also that the duplicates aren’t evenly distributed, the further you get the more work you have to do to get a value you haven’t seen before.

Of limited use I guess but if this is the kind of thing you need, pretty convenient. I’ve dumped the code I used to generate these in a gist.

→ 2 Comments

Posted in Uncategorized

Piping into a desktop indicator

Posted on April 14, 2015 | Leave a comment

This post is about interacting with the graphical desktop environment from a shell script. Specifically: say you have a long-running bash script and you’d like to keep an eye on it through a unity app indicator. How do you make that work in an appropriately unix-y way? (If you’re not sure what I mean see the animation below).

Background. Over the weekend I finally changed from NFS to rsync for keeping my source code in sync across machines. Much better if my network connection is unreliable and fewer moving parts. After I was done with the basics though I thought: I really need to be able to keep an eye on how syncing is going. It’s just the worst to spend ages unsuccessfully trying to reproduce an issue on a virtual machine only to realize that it’s because the code I’m running isn’t being properly synced when I edit files on my laptop.

Here’s what I had in mind: when I run the code change monitor shell script I want to get an app indicator in the top bar that changes state when a sync is going on, so I can see that syncing actually happening and whether it’s slow. And I want it to show if there are any errors. This, in other words

The syncing logic itself is straightforward: one component uses inotifywait to wait for files to change (watchdog.sh), then calls out to a script that does the actual sync (do-rsync.sh).

How to show the indicator though? There is no command-line api for this kind of thing and I wasn’t sure what it would look like if there was. Also, the existing code was properly unix-y and I wanted it to stay that way. One component knows how to wait for changes but knows nothing about rsync; the rsync part knows how to do a single sync but doesn’t care when or why it is being called. They only meet at the top level,

watchdog.sh --root . ./do-rsync.sh

What I ended up with was a python script, sync-indicator.py, that was responsible for just the indicator. When it starts it creates the indicator and then waits around, reading input from stdin. When it sees a command in the output it recognizes, say [SYNC: syncing], it consumes that line and changes the state of the indicator. Anything that doesn’t match is just passes straight through to stdout. Here’s what it looks like,

This way the indicator logic doesn’t need to know about the watching or rsyncing, and those parts don’t need to know about the indicator. All you need to do is change the toplevel command that puts it all together to,

watchdog.sh --root . ./do-sync-and-indicate.sh | ./sync-indicator.py

where do-sync-and-indicate.sh is a trivial wrapper around do-sync.sh that looks like this,

#!/bin/bash

echo "[SYNC: syncing]"
if ./do-sync.sh; then
  echo "[SYNC: idle]"
else
  echo "[SYNC: error]"
fi

You can even replace this with a generic command that takes another command as an argument and all it does is call that command surrounded with appropriate SYNC messages.

Pretty clean and unix-y I think, independent components and so on. The python indicator script itself, sync-indicator.py, is straightforward, only 60ish lines with comments.

The ease of supporting this makes me wonder though. Why aren’t long-running commands better at interacting with the desktop?

→ Leave a comment

Posted in Uncategorized

Making tea

Posted on January 14, 2015 | 1 Comment

This post is about the mathematics of making a good cup of tea. I drink a lot of tea and for a long time I would ignore the direction to use water below boiling, say 75° or 85°. Because – if you don’t have a boiler with a temperature setting how do you get water at less than 100°? Wait for it to cool? Come on!

Of course you can do it easily by adding cold water, you just have to figure out how much. While I was waiting for a delivery this morning I thought I’d look into that and it turned out to be a fun little practical application of the scientific method.

Theory 1: the average temperature

Let’s assume tap water is 22° and you add 500ml of it to the same amount of boiling water. My starting assumption was that the result will be 1l of water at the average of the two temperatures, 61°:

$t_r = \frac{100 \cdot 500 + 22 \cdot 500}{500 + 500}=61$

Put more generally, my theory was that if you mix water of two different temperatures then the temperature of the result will be the average over the two temperatures, where each temperature is weighted by the volume of water

$t_r = \frac{100 v_b + t_t v_t }{v_b + v_t}$

(Here $t_r$ is the resulting temperature of the water, $v_b$ is the amount of boiling water which will be 100°, $t_t$ is the temperature of tap water, and $v_t$ is the amount of tap water.)

If you measure the tap water temperature and know how much water your tea pot will hold you can solve for the amount of boiling and tap water to use to make any given water temperature. For instance, my tap water is 22° and my tea pot holds 700ml so the formula for how much to boil for a given temperature is,

$t_r = \frac{100 v_b + 22 (700 - v_b)}{700}$

$t_r = \frac{100 v_b + 22 \cdot 700 - 22 v_b}{700}$

$t_r = \frac{78 v_b + 22 \cdot 700}{700}$

$700 (t_r - 22) = 78 v_b$

$\frac{700}{78} (t_r - 22) = v_b$

So to get a pot full of 85° water, the amount of boiling water should be

$\frac{700}{78} (85 - 22) = 8.97 \cdot 63 = 565$

Boil 565ml, add the rest up to 700ml from the tap (that would be 135ml) and you’ve got 700ml of 85° water. That’s the theory.

Ok, so having solved the problem I went to make tea, my delivery having still not arrived (spoiler alert: it arrived while I was at the dentist, obviously). It turns out though that the theory doesn’t work. When I did it in practice it turned out that the water wasn’t 85°, it was 77°. Bummer. The theory is too simplistic.

Theory 2: the tea pot constant

The problem was fortunately obvious: I was pouring the water into a cold tea pot. The formula only says what happens to the water itself, it doesn’t take into account that it all ends up in a pot that’s initially at room temperature.

What I thought I’d do then was to model the effect of the cold pot as if it were extra tap water. How much exactly I don’t know, but it seems reasonable to expect that the cooling effect of a particular pot works basically the same way as if you’d added a bit of extra cold water. So we replace $v_t$ in the formula above, the amount of tap water, with $v_t + v_p$ , the amount of tap water and some additional amount, $v_p$ , to account for the pot,

$t_r = \frac{100 v_b + t_t (v_t + v_p) }{v_b + v_t + v_p}$

You have to determine $v_p$ experimentally, it is a property of a particular pot just like the volume. I determined it by pouring boiling water into the cool pot and then measuring the temperature; it had dropped to 90°. Using this I could find $v_p$ ,

$t_r = \frac{100 v_b + t_t (v_t + v_p) }{v_b + v_t + v_p}$

$90 = \frac{100 \cdot 700 + 22 (0 + v_p) }{700 + v_p}$

$90 \cdot 700 + 90 v_p = 100 \cdot 700 + 22 v_p$

$-10 \cdot 700 = -68 v_p$

$\frac{10 \cdot 700}{68} = v_p = 103$

In other words: the pot cools boiling water as much as adding 103ml of extra tap water.

Again, it’s just a theory that this makes sense, but it’s a theory we can test. Earlier, I mixed 565ml boiling and 135ml tap water and got 77° instead of the 85° I expected. What does the new theory predict will happen?

$t_r = \frac{100 v_b + t_t (v_t + v_p) }{v_b + v_t + v_p}$

$t_r = \frac{100 \cdot 565 + 22 \left( 135 + 103 \right) }{700 + 103} = 76.9$

That’s so close to the 77° that you’d almost think I fudged the numbers, but it’s really just a coincidence.

With this new and more plausible general formula we can plug in the values for my pot and water and get a specific formula for how much boiling and tap water to use to produce a particular temperature in my pot,

$t_r = \frac{100 v_b + 22 (700 - v_b + 103)}{700 + 103}$

$t_r = \frac{100 v_b + 22 \cdot 803 - 22 v_b}{803}$

$t_r = \frac{78 v_b + 22 \cdot 803}{803}$

$803 (t_r - 22) = 78 v_b$

$\frac{803}{78} (t_r - 22) = v_b$

It turns out to be the same as the one before except with 803 instead of 700. Using this formula, then, to get 85° water I need

$\frac{803}{78} (85 - 22) = 10.29 \cdot 63 = 648$

ml of boiling and the rest, 52ml, of tap. I tried this out and the result was… drumroll… 86°. So the formula seems to work. Yay!

Summary

So, to sum all this up, here’s how you apply the formulas in practice.

Measure how much water it takes to fill your pot, call that $v$ . Boil that much water and pour it into the pot. Measure the temperature and call that $t_p$ . Measure the temperature of your tap water, call that $t_t$ . Plug them into this formula to get the tea pot constant for your tea pot, $v_p$

$v_p = v \frac{t_p - 100}{t_t - t_p}$

Then, given a temperature $t_r$ , the amount of water to boil to get that temperature can be calculated by,

$v_b = \frac{(v+v_p) (t_r-t_t)}{100-t_t}$

And that’s it. You only have to calculate these once for a given pot so even though it’s a hassle, it’s a one time hassle. And it’s possible that most tea pots have approximately the same constant, in which case you can just assume that yours has the same one. But that’s for future research into the fertile field that is the science of tea.

Ironically, I got so caught up calculating the ideal amount of water that I never actually made tea, just water of different temperatures. I think I’ll go make some actual tea now.

→ 1 Comment

Posted in mathematics, misc

Why I find IEEE 754 frustrating

Posted on November 8, 2014 | 10 Comments

Programming languages new (Java) and old (Fortran), and their compilers, still lack competent support for features of IEEE 754 so painstakingly provided by practically all hardware nowadays. […] Programmers seem unaware that IEEE 754 is a standard for their programming environment, not just for hardware.

William Kahan

This post is the result of me, a language design guy, trying and failing to figure out how to provide language bindings for IEEE 754 in a modern language. The TL;DR is,

The basic model described in 754 is great, no complaints.
The licensing terms of the spec document are deeply problematic.
The language bindings are too specific and have an old-school procedural flavor that makes them difficult to apply to a modern language.
It would be much more useful to know the motivation behind the design, that way each language can find a solution appropriate for them.

The rest of the post expands on these points. First off I’ll give some context about 754 and floating-point support in general.

754

I want to start out by saying that IEEE 754 has been enormously helpful for the world of computing. The fact that we have one ubiquitous and well-designed floating-point model across all major architectures, not multiple competing and less well designed models, is to a large extent thanks to 754. It’s been so successful that it’s easy to overlook what an achievement it was. Today it’s the water we swim in.

But 754 is two things, what I’ll call the model and the bindings. The model is a description of a binary floating-point representation and how basic operations on that representation should work. The bindings are a description of how a programming language should make this functionality available to programmers. The model is the part that’s been successful. The bindings, as Kahan, the driving force behing 754, admits, not so much.

I’ll go into more detail about why the bindings are problematic in a sec, it’s the main point of this post, but first I want to take a broader look at floating-point support in languages.

Floating-point is hard

I’m not really a numerical analysis guy at all, my interest is in language design (though as it happens the most popular blog post I’ve ever written, 0x5f3759df, is also about floating-point numbers). What interests me about floating-point (FP from now on) is that a couple of factors conspire to make it particularly difficult to get right in a language.

Because floats are so fundamental, as well as for performance reasons, it’s difficult to provide FP as a library. They’re almost always part of the core of the language, the part the language designers design themselves.
Numerical analysis is hard, it’s not something you just pick up if you’re not interested in it. Most language designers don’t have an interest in numerical analysis.
A language can get away with incomplete or incorrect FP support. To quote James Gosling, “95% of the folks out there are completely clueless about floating-point.”

The goal of the binding part of 754 is, I think, to address the second point. Something along the lines of,

Dear language designers,
We know you’re not at home in this domain and probably regret that you can’t avoid it completely. To help you out we’ve put together these guidelines, if you just follow them you’ll be fine.

Much love,
The numerical analysts

I think this is a great idea in principle. So what’s the problem?

Licensing

The most immediate problem is the licensing on the 754 document itself. Have you ever actually read it? I hadn’t until very recently. Do you ever see links from discussions around FP into the spec? I don’t, ever. There’s a reason for that and here it is,

The document is simply not freely available. This alone is a massive problem. Before you complain that people don’t implement your spec maybe stop charging them $88 to even read it?

More insidiously, say I support 754 to the letter, how do I document it? What if I want to describe, in my language spec, under which circumstances a divideByZero is raised? This is what the spec says,

The divideByZero exception shall be signaled if and only if an exact infinite result is defined for an operation on finite operands. The default result of divideByZero shall be an ∞ correctly signed according to the operation [… snip …]

This sounds good to me as is. Can I copy it into my own spec or would that be copyright infringement? Can I write something myself that means the same? Or do I have to link to the spec and require my users to pay to read it? Even if I just say “see the spec”, might my complete implementation constitute infringement of a copyrighted structure, sequence, and organization? The spec itself says,

Users of these documents should consult all applicable laws and regulations. […] Implementers of the standard are responsible for observing or referring to the applicable regulatory requirements.

So no help there. In short, I don’t know how to create FP bindings that conform to 754 without exposing myself to a copyright infringement lawsuit in the US from IEEE. Sigh.

My first suggestion is obvious, and should have been obvious all along: IEEE 754 should be made freely available. Maybe take some inspiration from ECMA-262?

That’s not all though, there are issues with the contents of the spec too.

The spec is too specific

The main problem with how the bindings are specified is that they’re very specific. Here’s an example (my bold),

This clause specifies five kinds of exceptions that shall be signaled when they arise; the signal invokes default or alternate handling for the signaled exception. For each kind of exception the implementation shall provide a corresponding status flag.

What does it mean to provide a status flag? Is it like in JavaScript where the captures from the last regexp match is available through RegExp?

$ /.(.)./.exec("abc")
> ["abc", "b"]
$ RegExp.$1
> "b"

It looks like that’s what it means, especially if you consider functions like saveAllFlags,

Implementations shall provide the following non-computational operations that act upon multiple status flags collectively: [snip]

― flags saveAllFlags(void)
Returns a representation of the state of all status flags.

This may have made sense at the time of the original spec in 1985 but it’s mutable global state – something that has long been recognized as problematic and which languages are increasingly moving away from.

Here’s another example. It sounds very abstract but for simplicity you can think of “attribute” as roundingMode and “constant value” as a concrete rounding mode, for instance roundTowardsZero.

An attribute is logically associated with a program block to modify its numerical and exception semantics. […] For attribute specification, the implementation shall provide language-defined means, such as compiler directives, to specify a constant value for the attribute parameter for all standard operations in a block […].

Program block? Attribute specification? Nothing else in my language works this way. How do I even apply this in practice? If attributes are lexically scoped then that would mean rounding modes only apply to code textually within the scope – if you call out to a function its operations will be unaffected. If on the other hand attributes are dynamically scoped then it works with the functions you call – but dynamically scoped state of this flavor is really uncommon these days, most likely nothing else in your language behaves this way.

You get the picture. The requirements are very specific and some of them are almost impossible to apply to a modern language. Even with the best will in the world I don’t know how to follow them except by embedding a little mini-language just for FP that is completely different in flavor from the rest. Surely that’s not what anyone wants?

What do I want then?

As I said earlier, it’s not that I want to be left alone to do FP myself. I’m a language guy, almost certainly I won’t get this right without guidance. So what is it that I want?

I want the motivation, not some solution. Give me a suggested solution if you want but please also tell me what the problem is you’re trying to solve, why I’m supporting this in the first place. That way, if for some reason your suggested solution just isn’t feasible there’s the possibility that I can design a more appropriate solution to the same problem. That way at least there’ll be a solution, just not the suggested one.

For instance, it is my understanding that the rounding mode mechanism was motivated mainly by the desire to have a clean way to determine error bounds. (Note: as pointed out on HN and in the comments, the rest of this section is wrong. Something similar was indeed the motivation for the mechanism but not exactly this, and you don’t get the guarantees I claim you do. See the HN discussion for details.) It works like this. Say you have a nontrivial computation and you want to know not just a result but also the result’s accuracy. With the rounding mode model you’d do this: repeat the exact same computation three times, first with the default rounding, then round-positive (which is guaranteed to give a result no smaller than the exact result) and finally round-negative (which is guaranteed to give a result no larger). This will give you an approximate result and an interval that the exact result is guaranteed to be within. The attribute scope gymnastics are to ensure that you can replicate the computation exactly, the only difference being the rounding mode. It’s actually a pretty neat solution if your language can support it.

It’s also a use case that makes sense to me, it’s something I can work with and try to support in my own language. Actually, even if I can implement the suggested bindings exactly as they’re given in the spec the motivation is still useful background knowledge – maybe it’s a use case I’ll be extra careful to test.

I’m sure there are other uses for the binding modes as well. But even if I assume, wrongly, that there isn’t, that misapprehension is still an improvement over the current state where I have nothing to fall back to so I dismiss the whole rounding mode model outright.

(As a bitter side note, minutes from the 754-2008 revision meetings are available online and I expect they contain at least some of the motivation information I’m interested in. I don’t know though, I can’t search for the relevant parts because the site’s robots.txt prevents search engines from indexing them. Grr.)

In conclusion, I think the people who regret that languages don’t have proper support for 754 could do a lot to improve that situation. Specifically,

Fix the licensing terms on the spec document.
Describe the use cases you need support for, not just one very specific solution which is hard to apply to a modern language.
As an absolute minimum, fix the robots.txt so the spec meeting minutes become searchable.

(HN discussion, reddit discussion)

Update: removed sentence that assumed the spec’s concept of exceptions referred to try/except style exceptions. Don’t use the term “interval arithmetic” about determining error bounds.

→ 10 Comments

Posted in languages

Shift/Reduce Expression Parsing (by Douglas Gregor)

Posted on October 31, 2014 | 2 Comments

Once every few years I end up, for one reason or another, having to implement an operator precedence parser. Getting it right is a bit fiddly. I once found a great article about how you do it and tend to just follow that but a while ago that article disappeared.

Now, again, I find myself having to implement an operator precedence parser, in yet another language, and so I dug up the old article on archive.org and decided: since I find it super useful and it’s completely gone from the web, maybe I should just host a copy here. So here it is. It’s a design doc from the sugar parser library written by Douglas Gregor. So, to be clear, I didn’t write this doc I’m just reposting it here (with a few minimal formatting changes) because it’s good and that way it’s at least available somewhere.

If anyone, particularly Douglas Gregor, has an opinion or an objection please leave a comment.

Shift/Reduce Expression Parsing

Introduction

The Sugar expression parser is similar to the class of operator-precedence parsers, but has been extended to support common requirements when parsing expressions, such as function application, confix (grouping) operators, and operator name disambiguation. Additionally, Sugar is intended to be usable without any precompiling phase, making it ideal for rapid or on-the-fly construction of expression parsers.

Expressions

For the purposes of this document, an expression is a sequence of operators and operands, where operators fall into one of the following categories:

Type	Arity	Placement	Examples
Prefix	Unary	Prior to operand	Unary minus
Postfix	Unary	After operand	Factorial
Infix	Binary	Between operands	Addition, multiplication, and division
Confix	Unary	Surrounding operand	Parentheses, half-open ranges
Function application	Binary	After first operand and surrounding second operand	Mathemetical functions (sin(x)), array indexes(a[5])

The confix and function application operators are essentially split into their component parts, an open symbol and a close symbol, during the parsing phase. The “open” symbol will occur on the left-hand side and the “close” symbol will occur on the right-hand side.

Constructing the parser

The expression parser is a shift/reduce parser with zero lookahead that utilizes two separate stacks: one for operators and one for operands. Any operands in the input stream are immediately shifted onto the operator stack; operators are immediately shifted onto the operator stack only if the operator stack is empty. Otherwise, the following table determines the action of the parser depending on the type of the operator on top of the operator stack and on the type of the current operator token.

		Current operator
		Prefix	Postfix	Infix	Confix Open	Confix/Function Close	Function Open	End of Input
Top of Stack	Prefix	shift	precedence	precedence	shift	reduce	precedence	reduce
	Postfix	–	reduce	reduce	–	reduce	reduce	reduce
	Infix	shift	precedence	precedence/associativity	shift	reduce	precedence	reduce
	Confix Open	shift	shift	shift	shift	shift	shift	reduce
	Confix/Function Close	reduce	reduce	reduce	reduce	reduce	reduce	reduce
	Function Open	shift	shift	shift	shift	shift	shift	reduce

Description of parsing actions

A shift operation pushes the current operator token onto the operator stack.
A reduce operation pops the operator token off the top of the operator stack, and then pops the appropriate number of operands from the operand stack. Then the operator is applied to the operand(s) and the result is pushed back on the operand stack. Reduction of confix operators and of function application requires popping two operators off the operator stack.
A precedence operation compares determines the relative precedence of the operator on top of the operator stack (top) and the current operator (current).
- If top has a lower precedence than current, shift.
- If top has a higher precedence than current, reduce.
A precedence/associativity operation first compares the precedence according to the precedence operation: if the precedence is equivalent, associativity is considered:
- If top associates left of current, reduce.
- If top associates right of current, shift.

Rejecting Invalid Expresions

Operator-precedence parsers are often not used because they accept invalid strings. The shift-reduce parser as specified above will consider the expressions x + x, + x x, and x x + equivalent, even though only the first form is correct. This weakness is easily remedied with the use of the following state machine to track what type of operator or operand is expected at any given point in time.

The state machine contains three states: the pre-operand state where we collect confix open and prefix operators while waiting for an operand, the post-operand state where we have received an operand and are applying postfix operators to it and closing confix operators or finishing function calls, and finally an error state that will be entered when an invalid parse is detected.

Disambiguation of Operator Names

Within many domains, certain operators are reused in different contexts. Several obvious examples are the unary and binary minus operators that use the same symbol ‘-‘, the absolute-value confix operator that uses the symbol ‘|’ as both its open and close symbol, and the ‘+’ operator for regular expressions that is both a postfix positive closure operator and an infix operator for specifying alternatives.

Disambiguation of operator names is in many cases directly related to the state machine used to identify invalid sequences. Given any operator name, we determine the set of operator types that it may belong to. We then intersect this with the set of operator types that are valid at our current state within the state machine to determine role(s) this operator may play in this context. Several cases are left ambiguous by this intersection. These cases are considered below with either a specific resolution or are considered impossible by this class of parser.

Disambiguation at this phase requires lookahead of one additional token, and is also based on the state machine. Disambiguation is possible when the possible meanings of the operator differ in the states that will result from their interpretation. For instance, if a given operator is both postfix and infix, the postfix interpretation would remain in the post-operand state whereas the infix interpretation would transfer to the pre-operand state. Looking ahead one symbol, we can determine if the next symbol would be valid in either state: if it is valid in only one of the resulting states, we can disambiguate the prior (non-lookahead) symbol to ensure that the appropriate state is reached so that the lookahead symbol will not result in a parse error.

{prefix, confix open}: ambiguous (requires arbitrary lookahead).
{postfix, infix}: single lookahead disambiguation based on state.
{confix/function close, infix}: single lookahead disambiguation based on state.
{function open, infix}: ambiguous (requires arbitrary lookahead).
{postfix, confix/function close}: ambiguous (requires arbitrary lookahead).
{postfix, function open}: single lookahead disambiguation based on state.
{function open, function/confix close}: single lookahead disambiguation based on state.

Parsing Examples

Mathematical Expressions

Parse the expression x * |y+z| + -3^x^y using the standard mathematical rules for precedence and associativity.

State	Operand Stack	Operator Stack	Token	Token type	Action
Pre			x	operand	shift
Post	x		*	infix operator	shift
Pre	x	*	\|	confix open or confix close	disambiguate as confix open, shift
Pre	x	* (confix open \|)	y	operand	shift
Post	x y	* (confix open \|)	+	infix or prefix operator	disambiguate as infix, shift
Pre	x y	* (confix open \|) +	z	operand	shift
Post	x y z	* (confix open \|) (infix +)	\|	confix open or confix close	disambiguate as close, reduce
Post	x (y+z)	* (confix open \|)	\|	confix open or confix close	disambiguate as close, reduce
Post	x (\|y+z\|)	*	+	infix or prefix	disambiguate as infix, compare precedence, reduce
Post	(x * (\|y+z\|))		+	infix or prefix	disambiguate as infix, shift
Pre	(x * (\|y+z\|))	(infix +)	–	infix or prefix	disambiguate as prefix, shift
Pre	(x * (\|y+z\|))	(infix +) (prefix -)	3	operand	shift
Post	(x * (\|y+z\|)) 3	(infix +) (prefix -)	^	infix	compare precedence, shift
Pre	(x * (\|y+z\|)) 3	(infix +) (prefix -) ^	x	operand	shift
Post	(x * (\|y+z\|)) 3 x	(infix +) (prefix -) ^	^	infix	compare precedence, compare associativity, shift
Pre	(x * (\|y+z\|)) 3 x	(infix +) (prefix -) ^ ^	y	operand	shift
Post	(x * (\|y+z\|)) 3 x y	(infix +) (prefix -) ^ ^	end	end	reduce
Post	(x * (\|y+z\|)) 3 (x^y)	(infix +) (prefix -) ^	end	end	reduce
Post	(x * (\|y+z\|)) (3^(x^y))	(infix +) (prefix -)	end	end	reduce
Post	(x * (\|y+z\|)) (-(3^(x^y)))	(infix +)	end	end	reduce
Post	((x * (\|y+z\|)) + (-(3^(x^y))))	empty	end	end	accept

Douglas Gregor
Last modified: Sat Aug 18 12:46:13 EDT 2001

→ 2 Comments

Posted in misc

Poly-ranges in haskell

Posted on September 26, 2014 | Leave a comment

I’ve been reading Learn You a Haskell and got stuck on a tiny point at the beginning, in the section about ranges: you can’t have a range with more than one step value. This post is about what it might mean to allow multiple steps and how Charles Babbage might have had an opinion on this particular aspect of haskell’s design.

Here’s the whole paragraph from Learn You a Haskell,

To make a list containing all the natural numbers from 1 to 20, you just write [1..20]. [… snip …] Ranges are cool because you can also specify a step. What if we want all even numbers between 1 and 20? Or every third number between 1 and 20?

ghci> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]
ghci> [3,6..20]
[3,6,9,12,15,18]

It’s simply a matter of separating the first two elements with a comma and then specifying what the upper limit is. While pretty smart, ranges with steps aren’t as smart as some people expect them to be. You can’t do [1,2,4,8,16..100] and expect to get all the powers of 2. Firstly because you can only specify one step. And secondly because some sequences that aren’t arithmetic are ambiguous if given only by a few of their first terms.

The bold highlight is mine. This makes sense – how can the language guess that what you have in mind when you write [1, 2, 4, 8, 16..] is the powers of 2?

On the other hand though, just as a fun exercise, if you were to allow multiple step values how would you define them? Even though this is a highly specialized and modern language design question I know Charles Babbage would have understood it and I suspect he would have had an opinion.

A while ago I wrote a post about Babbage’s difference engine. The difference engine is basically an adder that calculates successive values of a polynomial by doing simple addition, using a technique called divided differences. This is described in full detail in that post but here’s a summary. Take a sequence of values of values of a polynomial, for instance the first four squares,

$\begin{tabular}{lcl} f(0) & = & 0 \\ f(1) & = & 1 \\ f(2) & = & 4 \\ f(3) & = & 9 \\ & \vdots & \end{tabular}$

You can then calculate the next values using just addition by calculating the differences between the initial values. To get the differences for a sequence you subtract each pair of values,

$\begin{tabular}{l|l} 0 \\ & 1 \\ 1 \\ & 3 \\ 4 \\ & 5 \\ 9 \end{tabular}$

Do it once and you get the first differences. Do the same thing to the first differences and you get the second differences,

$\begin{tabular}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 && 2\\ & 5 \\ 9 \end{tabular}$

Do the same thing to the second differences and you get the third differences,

$\begin{tabular}{l|l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 && 0\\ 4 && 2\\ & 5 \\ 9 \end{tabular}$

In this case there’s just one and it’s 0 so we can ignore it. Once you have all the differences you can calculate the next value of the polynomial by adding them together from right to left,

$\begin{tabular}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 && 2 \\ & 5 \\ 9 \end{tabular} \quad\to\quad \begin{tabular}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 && 2 \\ & 5 & \tiny{+0} \\ 9 && \bf{2} \end{tabular} \quad\to\quad \begin{tabular}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 && 2 \\ & 5 \\ 9 & \tiny{+2} & \bf{2} \\ & \bf{7} \\ \end{tabular} \quad\to\quad \begin{tabular}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 && 2 \\ & 5 \\ 9 && \bf{2} \\ \tiny{+7} & \bf{7} \\ \bf{16} \\ \end{tabular}$

There it is, 16, the next value in the sequence. At this point we can just keep going,

$\begin{tabular}{l|l|l} \multicolumn{1}{r}{}&&2 \\ & 7 & \tiny{+0}\\ 16 &\tiny{+2}& 2 \\ \tiny{+9} & 9 \\ \bf{25} \\ \end{tabular} \quad\to\quad \begin{tabular}{l|l|l} \multicolumn{1}{r}{}&&2 \\ & 9 & \tiny{+0}\\ 25 &\tiny{+2}& 2 \\ \tiny{+11} & 11 \\ \bf{36} \\ \end{tabular} \quad\to\quad \begin{tabular}{l|l|l} \multicolumn{1}{r}{}&&2 \\ & 11 & \tiny{+0}\\ 36 &\tiny{+2}& 2 \\ \tiny{+13} & 13 \\ \bf{49} \\ \end{tabular} \quad\to\quad\dots$

This technique works for any polynomial. The difference engine was given its name because it is a mechanical implementation of it.

Already you may suspect how this can be relevant to ranges in haskell. You can generalize ranges to n step values by using divided differences on the step values to generate the rest of the sequence. With two step values the result of this is a linear sequence, as you would expect (polyEnumFrom is my name for the generalized range function),

ghci> polyEnumFrom [0, 1]
[0, 1, 2, 3, 4, 5, 6, ...]
ghci> polyEnumFrom [4, 6]
[4, 6, 8, 10, 12, 14, 16, ...]
ghci> polyEnumFrom [10, 9]
[10, 9, 8, 7, 6, 5, 6, ...]

Give it three elements, for instance the squares from before, and the result is a second-order polynomial,

ghci> polyEnumFrom [0, 1, 4]
[0, 1, 4, 9, 16, 25, 36, ...]

Similarly with the cubes,

ghci> polyEnumFrom [0, 1, 8, 27]
[0, 1, 8, 27, 64, 125, 216, ...]

There is nothing magical going on here to recognize the squares or cubes here, it’s a completely mechanical process that uses subtraction to get the differences and addition to then continue the sequence past the step values. It won’t give you the squares though, only polynomials. If you try you get

ghci> polyEnumFrom [1, 2, 4, 8, 16]
[1, 2, 4, 8, 16, 31, 57, ...]

For any list of 3 step values there is exactly one polynomial of order 2 or less that yields those values; an order-2 polynomial has 3 free variables so there’s no room for more than one solution. The result of a 3-step range is the sequence of values produced by that order-2 polynomial. In general, the result of a multi-step range with n steps is the sequence of values generated by the unique polynomial of order at most n-1 whose first n values are the steps. Conveniently, if the steps are integers the polynomial is guaranteed to only produce integers.

Babbage built the difference engine because it was really important then be able to produce tables of function values by calculating successive values of polynomials. I think he would have appreciated the power of a language where you can condense the work of generating an approximate table of sine values into a single line,

take 10 (polyEnumFrom [0, 0.0002909, 0.0005818, 0.0008727])

which yields,

0.0000000
0.0002909
0.0005818
0.0008727
0.0011636
0.0014545
0.0017454
...

(The four values given to polyEnumFrom are the first four sine values from the table.) Of course, Babbage did lose interest in the difference engine himself and preferred to work on the more general analytical engine. If he did see haskell he would probably quickly lose interest in ranges and move on to more general advanced features. But I digress.

Is a shorthand for sequences of polynomial values actually a useful feature in a language? I doubt it. But I like the idea that a corner of a modern language intersects with Babbage and the difference engine. Maybe it would make sense as a little easter-egg tribute to Babbage, a difference engine hiding behind a familiar language construct. I quite like the idea of that.

If you want to play around with it I’ve put an implementation in a gist. For something that might seem fairly complex the implementation is simple – polyEnumFrom and its helpers is just 13 lines. Haskell is an elegant language.

→ Leave a comment

Posted in Uncategorized

Hummus and Magnets

Bitwise division

Let’s generalize

Appendix

World history is off by one

What’s in a millennium?

Jesus!

Year Zero

How about this?

More Than Voronoi

Stdout is a dead end

A simple way to pre-scramble a sequence

Piping into a desktop indicator

Making tea

Theory 1: the average temperature

Theory 2: the tea pot constant

Summary

Why I find IEEE 754 frustrating

754

Floating-point is hard

Licensing

The spec is too specific

What do I want then?

Shift/Reduce Expression Parsing (by Douglas Gregor)

Shift/Reduce Expression Parsing

Introduction

Expressions

Constructing the parser

Description of parsing actions

Rejecting Invalid Expresions

Disambiguation of Operator Names

Parsing Examples

Mathematical Expressions

Poly-ranges in haskell

About me

Recent Posts

Posts by date

Posts by category