Programming languages new (Java) and old (Fortran), and their compilers, still lack competent support for features of IEEE 754 so painstakingly provided by practically all hardware nowadays. […] Programmers seem unaware that IEEE 754 is a standard for their programming environment, not just for hardware.
This post is the result of me, a language design guy, trying and failing to figure out how to provide language bindings for IEEE 754 in a modern language. The TL;DR is,
- The basic model described in 754 is great, no complaints.
- The licensing terms of the spec document are deeply problematic.
- The language bindings are too specific and have an old-school procedural flavor that makes them difficult to apply to a modern language.
- It would be much more useful to know the motivation behind the design, that way each language can find a solution appropriate for them.
The rest of the post expands on these points. First off I’ll give some context about 754 and floating-point support in general.
754
I want to start out by saying that IEEE 754 has been enormously helpful for the world of computing. The fact that we have one ubiquitous and well-designed floating-point model across all major architectures, not multiple competing and less well designed models, is to a large extent thanks to 754. It’s been so successful that it’s easy to overlook what an achievement it was. Today it’s the water we swim in.
But 754 is two things, what I’ll call the model and the bindings. The model is a description of a binary floating-point representation and how basic operations on that representation should work. The bindings are a description of how a programming language should make this functionality available to programmers. The model is the part that’s been successful. The bindings, as Kahan, the driving force behing 754, admits, not so much.
I’ll go into more detail about why the bindings are problematic in a sec, it’s the main point of this post, but first I want to take a broader look at floating-point support in languages.
Floating-point is hard
I’m not really a numerical analysis guy at all, my interest is in language design (though as it happens the most popular blog post I’ve ever written, 0x5f3759df, is also about floating-point numbers). What interests me about floating-point (FP from now on) is that a couple of factors conspire to make it particularly difficult to get right in a language.
- Because floats are so fundamental, as well as for performance reasons, it’s difficult to provide FP as a library. They’re almost always part of the core of the language, the part the language designers design themselves.
- Numerical analysis is hard, it’s not something you just pick up if you’re not interested in it. Most language designers don’t have an interest in numerical analysis.
- A language can get away with incomplete or incorrect FP support. To quote James Gosling, “95% of the folks out there are completely clueless about floating-point.”
The goal of the binding part of 754 is, I think, to address the second point. Something along the lines of,
Dear language designers,
We know you’re not at home in this domain and probably regret that you can’t avoid it completely. To help you out we’ve put together these guidelines, if you just follow them you’ll be fine.Much love,
The numerical analysts
I think this is a great idea in principle. So what’s the problem?
Licensing
The most immediate problem is the licensing on the 754 document itself. Have you ever actually read it? I hadn’t until very recently. Do you ever see links from discussions around FP into the spec? I don’t, ever. There’s a reason for that and here it is,
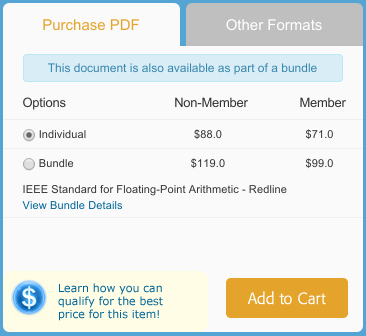
The document is simply not freely available. This alone is a massive problem. Before you complain that people don’t implement your spec maybe stop charging them $88 to even read it?
More insidiously, say I support 754 to the letter, how do I document it? What if I want to describe, in my language spec, under which circumstances a divideByZero is raised? This is what the spec says,
The divideByZero exception shall be signaled if and only if an exact infinite result is defined for an operation on finite operands. The default result of divideByZero shall be an ∞ correctly signed according to the operation [… snip …]
This sounds good to me as is. Can I copy it into my own spec or would that be copyright infringement? Can I write something myself that means the same? Or do I have to link to the spec and require my users to pay to read it? Even if I just say “see the spec”, might my complete implementation constitute infringement of a copyrighted structure, sequence, and organization? The spec itself says,
Users of these documents should consult all applicable laws and regulations. […] Implementers of the standard are responsible for observing or referring to the applicable regulatory requirements.
So no help there. In short, I don’t know how to create FP bindings that conform to 754 without exposing myself to a copyright infringement lawsuit in the US from IEEE. Sigh.
My first suggestion is obvious, and should have been obvious all along: IEEE 754 should be made freely available. Maybe take some inspiration from ECMA-262?
That’s not all though, there are issues with the contents of the spec too.
The spec is too specific
The main problem with how the bindings are specified is that they’re very specific. Here’s an example (my bold),
This clause specifies five kinds of exceptions that shall be signaled when they arise; the signal invokes default or alternate handling for the signaled exception. For each kind of exception the implementation shall provide a corresponding status flag.
What does it mean to provide a status flag? Is it like in JavaScript where the captures from the last regexp match is available through RegExp?
$ /.(.)./.exec("abc")
> ["abc", "b"]
$ RegExp.$1
> "b"
It looks like that’s what it means, especially if you consider functions like saveAllFlags,
Implementations shall provide the following non-computational operations that act upon multiple status flags collectively: [snip]
― flags saveAllFlags(void)
Returns a representation of the state of all status flags.
This may have made sense at the time of the original spec in 1985 but it’s mutable global state – something that has long been recognized as problematic and which languages are increasingly moving away from.
Here’s another example. It sounds very abstract but for simplicity you can think of “attribute” as roundingMode and “constant value” as a concrete rounding mode, for instance roundTowardsZero.
An attribute is logically associated with a program block to modify its numerical and exception semantics. […] For attribute specification, the implementation shall provide language-defined means, such as compiler directives, to specify a constant value for the attribute parameter for all standard operations in a block […].
Program block? Attribute specification? Nothing else in my language works this way. How do I even apply this in practice? If attributes are lexically scoped then that would mean rounding modes only apply to code textually within the scope – if you call out to a function its operations will be unaffected. If on the other hand attributes are dynamically scoped then it works with the functions you call – but dynamically scoped state of this flavor is really uncommon these days, most likely nothing else in your language behaves this way.
You get the picture. The requirements are very specific and some of them are almost impossible to apply to a modern language. Even with the best will in the world I don’t know how to follow them except by embedding a little mini-language just for FP that is completely different in flavor from the rest. Surely that’s not what anyone wants?
What do I want then?
As I said earlier, it’s not that I want to be left alone to do FP myself. I’m a language guy, almost certainly I won’t get this right without guidance. So what is it that I want?
I want the motivation, not some solution. Give me a suggested solution if you want but please also tell me what the problem is you’re trying to solve, why I’m supporting this in the first place. That way, if for some reason your suggested solution just isn’t feasible there’s the possibility that I can design a more appropriate solution to the same problem. That way at least there’ll be a solution, just not the suggested one.
For instance, it is my understanding that the rounding mode mechanism was motivated mainly by the desire to have a clean way to determine error bounds. (Note: as pointed out on HN and in the comments, the rest of this section is wrong. Something similar was indeed the motivation for the mechanism but not exactly this, and you don’t get the guarantees I claim you do. See the HN discussion for details.) It works like this. Say you have a nontrivial computation and you want to know not just a result but also the result’s accuracy. With the rounding mode model you’d do this: repeat the exact same computation three times, first with the default rounding, then round-positive (which is guaranteed to give a result no smaller than the exact result) and finally round-negative (which is guaranteed to give a result no larger). This will give you an approximate result and an interval that the exact result is guaranteed to be within. The attribute scope gymnastics are to ensure that you can replicate the computation exactly, the only difference being the rounding mode. It’s actually a pretty neat solution if your language can support it.
It’s also a use case that makes sense to me, it’s something I can work with and try to support in my own language. Actually, even if I can implement the suggested bindings exactly as they’re given in the spec the motivation is still useful background knowledge – maybe it’s a use case I’ll be extra careful to test.
I’m sure there are other uses for the binding modes as well. But even if I assume, wrongly, that there isn’t, that misapprehension is still an improvement over the current state where I have nothing to fall back to so I dismiss the whole rounding mode model outright.
(As a bitter side note, minutes from the 754-2008 revision meetings are available online and I expect they contain at least some of the motivation information I’m interested in. I don’t know though, I can’t search for the relevant parts because the site’s robots.txt prevents search engines from indexing them. Grr.)
In conclusion, I think the people who regret that languages don’t have proper support for 754 could do a lot to improve that situation. Specifically,
- Fix the licensing terms on the spec document.
- Describe the use cases you need support for, not just one very specific solution which is hard to apply to a modern language.
- As an absolute minimum, fix the robots.txt so the spec meeting minutes become searchable.
(HN discussion, reddit discussion)
Update: removed sentence that assumed the spec’s concept of exceptions referred to try/except style exceptions. Don’t use the term “interval arithmetic” about determining error bounds.