Tables

I have a thing for mechanical calculators and it recently occurred to me that I knew almost nothing about two of the most famous ones: Babbage’s difference engine and analytical engine. This led me to read some of the papers from the mid 1800s that were written about them. This blog post is the first of a few I’m planning to write about that.

The analytical engine usually gets most of the attention but the difference engine is an interesting invention in its own right. Not only did it solve an important problem, it is the only one of the two that was complete enough to actually be built. This post about what made the difference engine so important that Babbage spent decades trying to build it and why British government was willing to pay the bill of over ₤17,000, more than the price of two warships.

Calculation

Today computation is cheap. Extremely cheap. Imagine the amount of math that goes into just displaying the image on your screen right now: the layouts, colors, and fonts, rendering it all on a physical display, and doing it again and again quickly and smoothly enough that you don’t even notice it’s happening.

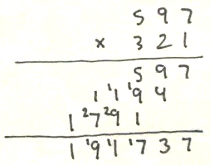
Computation is so cheap that it’s easy to forget how expensive it was before electronic calculators. It used to be that if you wanted to add two numbers together you had to actually add those numbers together. Manually. Need to multiply or divide two numbers, even just a few digits? Then you’ll have to get the paper out and do long multiplication or long division. I just did a long multiplication to make the image on the right here. I got it wrong twice before getting it right and I went from “this’ll be fun, I wonder if I still remember how to do this” to “god this is so tedious” in about 30 seconds.

And those are just the basic building blocks of doing a calculation. Most interesting computations like calculating interest or the position of the moon in six months require you to do these manual computations over and over and over again. Or require operations that you can’t easily calculate by hand, like trigonometric functions.

At this point you might be thinking: who cares where the moon is in six months? It turns out, back in those days a lot of people did. In some cases people’s lives depended on it.

Lunar Navigation

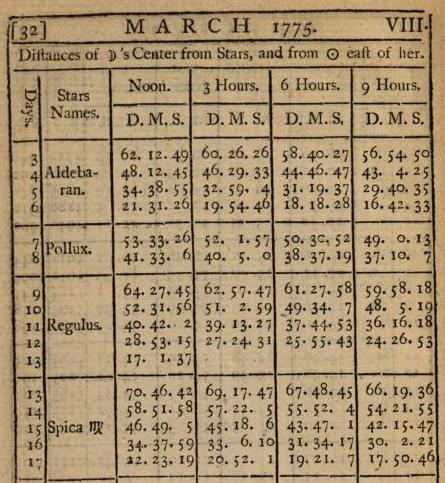
On the right here is a table of distances in degrees on the night sky from the center of the moon to various stars at particular times. The first line gives the distance between the center of the moon and Aldebaran on March 3, 1775 at noon, 3, 6, and 9 o’clock. Multiply that by 365 days, then multiply it by a dozen stars, that gives you just some of the tables in this book, the first edition of the Nautical Almanc and Astronomical Ephemeris from 1774, published from the Royal Greenwich Observatory. The audience for the almanac were mariners. The first edition of 10,000 copies sold out immediately.

To determine your longitude at sea you need to know the current time at a fixed point. You can think of it sort of like navigating with time zones. If you know it’s 4 o’clock in the afternoon Greenwich and it’s noon where you are (which you can tell by looking at the sun) then you know you’re in the -4 time zone which is the one that goes through eastern Canada, the eastern Caribbean and central South America. This is a rough analogy but that’s the gist of how it works.

Up until around 1850, before accurate clocks were made that could be carried on long voyages, a reliable way to determine the current time was using lunar distance. The moon and stars in the night sky move as a perfectly predictable clockwork. A given configuration occurs only once, and you can calculate in advance precisely what the sky is going to look like at a later time. And more importantly you can go the other way: given the precise configuration of the sky you can calculate exactly what time it is.

Actually you don’t need the full configuration; all you need to know to calculate the time is the distance in degrees from the center of the moon to any star. That’s where the almanac comes in. It precomputes those distances so that all a navigator needs to do is measure the angle (typically using a sextant) and then look the value up in the almanac. Okay that’s actually just the basic principle, there’s a lot more to it in practice: you have to adjust for the distance from the center of the moon to the circumference, for your position on the earth, for atmospheric refraction, etc. Being a navigator takes a lot of skill. How do you make those adjustments by the way? More tables of course.

All this means that having accurate tables is extremely important. An undetected error in the almanac means a navigation error which can mean shipwreck. This is made worse because many of these tables are time dependent: one line in the almanac is useful on one day only. As a navigator you’re basically beta testing the data for every single day because nobody has had any reason to use the data before.

There are many sources of errors in numerical tables. Teams of human computers carried out the manual calculations, a tedious and error prone process. (Incidentally, it turns out that the better an understand you have of the calculation you’re carrying out the more likely you are to make mistakes as a computer.) Often the same value would be calculated by more than one human computer and then compared to catch errors – but checking is an error prone process in itself, and computers can (and did) copy from each other. Then finally someone has to manually set the values in movable type and print them, also an obvious source of errors.

Enter Charles Babbage.

Babbage

Babbage was an unorthodox and very gifted mathematician. He was a fan of Leibniz which was still something of a heresy at his college Trinity, home of Newton, Leibniz’s arch rival. He was also one of the founders of the Analytical Society whose goal it was to replace Newton’s formalism for calculus with Leibniz’s. Incidentally, besides inventing calculus independently from Newton Leibniz designed a mechanical calculating machine, the stepped reckoner.

Babbage recognized the problem of calculating tables, as most people did, but also had a solution: the difference engine. The idea behind the difference engine is that most of the functions you want to create tables for can be approximated by a polynomial. Here is the sine function along with three approximating polynomials of increasing degree:

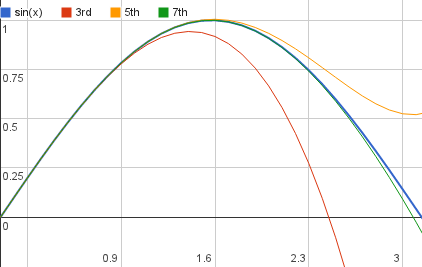
As the degree of the polynomial increases the approximation quickly becomes better – the degree-seven polynomial is quite close:

\[f_7(x) = x - \frac{x^3}{3!} + \frac{x^3}{5!} - \frac{x^7}{7!}\]

Babbage’s idea was to use mechanical means to calculate the approximating polynomials with high accuracy not just print the result on paper but do the actual typesetting to eliminate even the typographer as a source of errors.

But I’ll stop here before we get to the juicy details of how the difference engine works and save that for my next blog post.