Z-Quads: Strings
This post is about giving a memorable name to every spot on the earth. It’s the fourth and probably last post in my series about z-quads, a spatial coordinate system. Previously I’ve written about their basic construction, how to determine which quads contain each other, and how to convert to and from geographic positions. This post describes a scheme for converting a quad to a memorable name and back again.
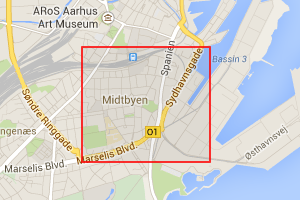
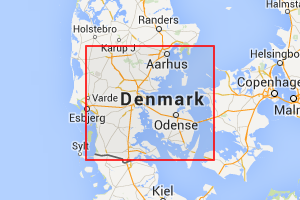
Above are two examples. The left image is quad 10202 whose name is naga. The second is quad 167159511 whose name is naga hafy. As you might expect, naga hafy is contained within naga.
I can understand if at this point you’re thinking: what could possibly be the point of giving a nonsense name to every square on the surface of the earth?
What it’s really about is hacking your brain a little bit, encoding data using a pattern the brain is good at remembering instead of raw numbers which it isn’t. My original motivation was Ukendt Aarhus who takes pictures at inaccessible places in Århus and posts them on facebook, along with the position they were taken. I saw some of the pictures in real life and had to type a position like this
56.154382 / 10.20489
into google maps on my phone. My brain has absolutely no capacity for remembering numbers, even for a short while, so I have to do it a few digits at a time, looking back and forth. I’m much better at remembering words, even nonsense words. That is, I can hold more of this,
in my head at once. Not the whole thing but certainly one word at a time, sometimes two. That’s the effect this naming scheme aims to use. Three words gives you a fairly precise location (a ~10m square) and if you need less, say to identify the location of a city, two words (a ~1km square) is typically enough. The town I grew up in, which is very small indeed, is uniquely identified by naga opuc.
Salad words
How do you generate reasonably memorable names automatically? The trick I used here is the one I usually use: alternate between consonants and vowels. It doesn’t always work but is usually good enough. I call those salad words (because “salad” is one).
If you use just the English alphabet you have 6 vowels and 20 consonants. You can make 28800 four-letter salad words with those: two vowels (62) times two consonants (202) times 2 for whether the word starts with a consonant or a vowel. There are 21845 quads on the first 7 zoom levels so that will fit in one four-letter salad word.
The first step in generating the string representation of a quad, then, is to split it into chunks that each hold 7 zoom levels. So if you want to convert quad 171171338190 which is at zoom level 19 you divide it into two chunks at level 7 and one chunk at level 5
10202 9941 974
This can be done using the ancestor/descendency operations from earlier. You can then convert each chunk into a word separately.
Encoding a chunk
There are many ways you could mape a value between 0 and 21845 to a salad word but one property I’d like the result to have is that it should give some hint about which area it covers, very roughly at least. I ended up with the following decomposition, (and let’s use zagi as an example while I describe how it works).
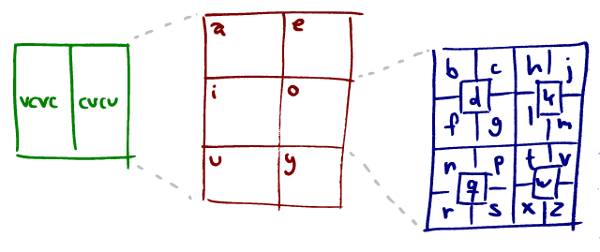
The world is divided into two parts along the Greenwich meridian. To the west words are vowel-consonant-vowel-consonant, to the east they’re consonant-vowel-consonant-vowel. So zagi must be east of Greenwich.
Each half is divided into six roughly evenly sized parts which determines what the first vowel is. (Note: not the first letter, the first vowel, which can be either the first or second letter.) The first vowel in zagi is a so it must be in the northwestern part of the eastern hemisphere. Each of the six divisions are subdivided 20 ways which determines the first consonant. The first consonant in zagi is z which is way down in the bottom right corner. This puts the location almost exactly in the middle of the eastern hemisphere. In fact, zagi is the quad that covers New Delhi.
The last two letters are determined in a similar way, further subdividing the region:
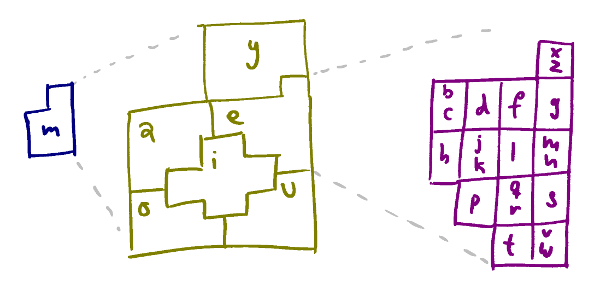
The second vowel determines a further subdivision, the second consonant narrows the quad down fully.
Now, the point of this is not for it to be possible to look at the name of a quad and know where it is – though the word ordering and first vowel rule sticks in your head pretty easily. The property it does have though is that at every level you have similar words grouped together geographically. These four maps show all level-7 quads that start with o, then on, then one, then finally onel.
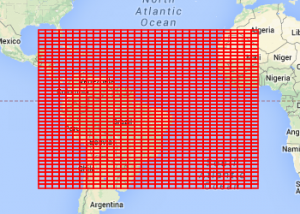
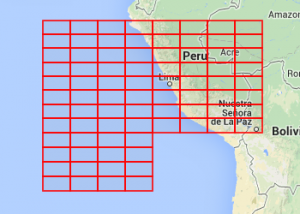
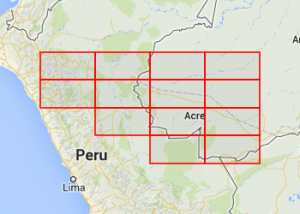
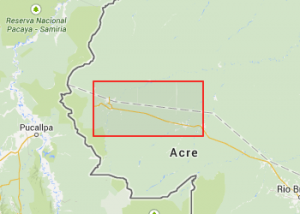
If you know where onel is then you can be sure that onem is somewhere nearby.
The basic scheme is an attempt to exploit that we’re better at remembering word-like data than raw numbers. The subdivision scheme is a way to take that further and put some more patterns into the data. The brain is great at recognizing patterns.
In my experience it serves its purpose well: if you’re working within a particular area you become somewhat familiar with the quads by name and it becomes easier to remember things about them. One example is that coincidentally, Arizona is covered by quads starting with az, which is easy to remember. That gives you an anchor that helps you locate other a-quads because all the second consonants are located in a predictable way relative to each other. If you know where one is, that gives you a sense of where the others are.
I didn’t plan for that particular rule to be possible, I just noticed that I had started using it. And that’s the point: the patterns aren’t intended to be used or recognized in any particular way that I’ve anticipated in advance. They’re just available, like the grid on graph paper. How you actually remember them, or if you do at all, only emerges when you use the system in practice.
Implementation
The actual encoding/decoding is pretty straightforward but it’s tedious so I won’t go through it in detail, it’s in the source (js/java) if you’re curious. The shapes of the irregular subdivisions are encoded as a couple of tables.
The one bit that isn’t straightforward is the scheme for encoding the zoom levels 0-6. Remember, we’re not just encoding one zoom level but 8 of them. The trick when encoding a quad at the higher levels, 0-6, is to take the quad’s midpoint and zoom it down to level 7, keeping a bit saying whether we zoomed or not. Then encode the first three letters as if it were a level 7 quad initially and finally use the zoomed/not-zoomed bit to determine the last consonant. This is why there are two consonants in some of the cells in the purple diagram for the last consonant above. This works because if you take the midpoint of a quad levels 0-z and find cell at level z+1 that contains it, no other midpoint from 0-z will land in that same cell. So it’s enough to know whether we zoomed or not, if we did then there is a unique ancestor which must be the one we zoomed from.
Four-letter words
Another wrinkle on this scheme is that some four-letter salad words are, well, rude. Words you’d probably rather avoid if you have the choice. Since we’re only using 21845 of the 28800 possible words it’s easy to find an unused word near any one you’d like to avoid and manually map, for instance, 6160 to anux rather than anus.
There are many four-letter salad words left with meaning, even if you remove the rude ones. Like tuba, epic, hobo, and pony. Only 70% of words correspond to a valid quad so 30% of the meaningful words will not be valid. Of the ones that do a lot of them of them will be somewhere uninteresting like the ocean or Antarctica. But some do cover interesting places: pony and sofa are in WA, Australia, atom is near Vancouver, toga is in Papua New Guinea.
The toy site I mentioned in the last post also allows you to play around with quad names. Here is pony tuba,
The URL is,
http://zquad.p5r.org?name=pony-tuba
Further exploration
There’s a lot more you can do with z-quads, both as mathematical objects and as data structures.
On the data structure side spatial data structures and quad trees are well understood and it’s unclear how much new, if anything, you can do with z-quads. In my experience though they’re a convenient handle to use to describe and address data within spatial data structures.
As mathematical objects they have some nice properties and if you want to prove properties about them – for instance that a quad can contain at most one midpoint of a higher-level quad – they’re friendly to induction proofs. You can also easily generalize them, for instance to any number of coordinates. If you want to represent regular cubes instead of squares all the same tools work, they just have to be tweaked a bit:
b3z = 1 + 8 + … + 8z-1 + 8z
ancestor3(q, n) = (q – b3z) / 8n
The other way works too, with one dimension instead of two. That model gives you regular divisions of the unit interval.
This will probably be my last post about them though. It’s time to get back to coding with them, rather than writing about them.