Bezier
A while ago I got it into my head that I should see if it was possible to render vector graphics on an LCD display driven by an Arduino. Over christmas I finally had some time to give it a try and it turns out that it is possible. Here’s what it looks like.
What you’re seeing there is a very stripped down version of SVG rendered by an Arduino. The processor driving it is 16 MHz and has only 2K of RAM so doing something as computationally expensive as rendering vector graphics is a bit of a challenge. Here’s what a naive implementation with no tuning looks like:
This post is about how the program works and mainly about how I got from the slow and blocky to the much faster and smoother version.
Hardware setup

On the right here is the hardware I’m using (click for a larger image). It’s an Arduino Uno connected to an 1.8” TFT LCD display, 160 by 128 18-bit color pixels, and two 2-axis joysticks for navigating. The zooming, rotating, and panning you saw in the videos above was controlled by the joysticks: the top one pans up/down and left/right, the bottom one zooms in and out when you move it up and down and rotates when you move it left and right. I had the Arduino already and the rest, the display and joysticks, cost me around $45.
Software setup
If you open an .svg file you’ll see that path elements are specified using a graphical operation format that looks something like this
m 157.10609,48.631198
c 0,37.817019 -51.99553,51.899082 -77.682505,13.390051
C 52.802707,101.94644 2.8939181,85.209645 2.8939181,48.57149
c 0,-36.638156 49.6730159,-54.2537427 76.5296669,-13.344121
l 25.451205,-40.4365453 77.682505,-24.41472 77.682505,13.403829
z
Each line is a graphical operation: m is moveTo, c is curveTo, l is lineTo, etc. Lower-case indicates that the coordinates are relative to the endpoint of the last operation, upper-case means that the coordinates are absolute.
The first step was to get this onto the Arduino so I wrote a python script that switched to using purely absolute coordinates and output the operations as a C data structure:
PROGMEM static instr_t path[] = {
move_to(e(0.0), e(0.0), e(157.10609), e(48.631198)),
curve_to(e(157.10609), e(48.631198), e(157.10609), e(86.448217), ...),
curve_to(e(79.423585), e(62.021249), e(52.802707), e(101.94644), ...),
curve_to(e(2.8939181), e(48.57149), e(2.8939181), e(11.933334), ...),
line_to(e(79.423585), e(35.227369), e(104.87479), e(-5.2091763)),
line_to(e(104.87479), e(-5.2091763), e(182.557295), e(-29.6238963)),
line_to(e(182.557295), e(-29.6238963), e(260.2398), e(-16.2200673)),
line_to(e(260.2398), e(-16.2200673), e(157.10609), e(48.631198)),
end()
};
The macros, move_to, curve_to, etc., insert a tag in front of the coordinates. The result is like a bytecode format that encodes the path as a sequence of doubles. The main program runs through the path and renders it, one operation at a time, onto the display. Once it’s done it starts over again.
To implement navigation there is a transformation matrix that is updated based on the state of the joysticks and multiplied onto each of the the coordinates before they’re drawn. For details of how the matrix math works see the source code on github.
This is the same basic program that runs everything, from the very basic version to the heavily optimized version you saw at the beginning – the difference is how tuned the code is.
The display comes with a library that allows you to draw simple graphics like circles, straight lines, etc., and that’s what the drawing routines were initially based on. What it doesn’t come with is an operation for drawing curves so the main challenge was to implement curve_to.
Bezier curves
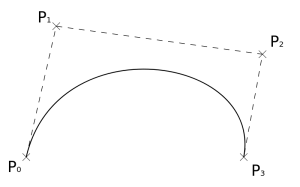
The SVG curve_to operation draws a cubic Bezier curve. I’m going to assume that you already know what a Bezier curve is so this is just a reminder. A cubic Bezier curve is defined by four points: start, end, and two control points, like you see here on the right. It goes from the start point to the end point and along the way gravitates towards first the one control point, then the second one, nice and smoothly.
If you’re given four points, let’s call them \(P_0=(x_0, y_0)\), \(P_1=(x_1, y_1)\), and so on, the Bezier defined by them is given by these parametric curves in x and y for t going between 0 and 1:
\[x = f_x(t) = x_0(1-t)^3 + 3x_1t(1-t)^2 + 3x_2t^2(1-t) + x_3t^3\] \[y = f_y(t) = y_0(1-t)^3 + 3y_1t(1-t)^2 + 3y_2t^2(1-t) + y_3t^3\]I’ll spend some more time working with this definition in a bit and rather than write two equations each time, one for x and one for y, I’m going to use the 2-element vector \(P=(x, y)\) instead so I can write:
\[P = f(t) = P_0(1-t)^3 + 3P_1t(1-t)^2 + 3P_2t^2(1-t) + P_3t^3\]It means the same as the x and y version but is shorter.
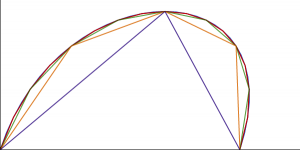
Using this definition you can draw a decent approximation of any Bezier curve just by plugging in values of t and drawing straight lines between the points you get out. The smoother you want the curve to be the more line segments you can use. On the right here is an example of using 2, 4, 8, 16, and 32 straight line segments. And on a small LCD you don’t need that many to get a decent-looking result.
First attempts
The graphics library that comes with the LCD supports drawing straight lines so it’s easy to code up the segment approach. On the right is the same video from before of what that looks like with 2 segments per curve. The way it works is that it clears the display, then draws the curve from one end to the other, and then repeats. As you can see it looks awful. It’s so slow that you can see how it constantly refreshes.
The problem is the size and depth of the display. With 160 by 128 at 18-bit colors you need 45K just to store the display buffer – and the controller only has 2K of memory. So instead of buffering the line drawing routine sends each individual pixel to the display immediately. Writing a block of data is reasonably fast (sort of, I’ll get back to that later) but writing individual pixels is painfully slow.
Luckily, for what I want to do I really don’t need full colors, monochrome is good enough, so that reduces the memory requirement dramatically. At 1-bit depth 160 by 128 pixels is still more than we can fit in memory but it’s small enough though that half does fit. So the first improvement is to buffer half the image, flush it to the display in one block, then clear the buffer, buffer the second half and then flush that.
As you can see that already looks a lot better. The biggest improvement is that there’s no need to clear the display between updates so you don’t see it refreshing at all unless you move the image. Refreshing is also a lot faster because the program takes advantage of sending whole blocks of data. But the drawing is still quite coarse, and refreshing is slow. There is also a short but visible pause between rendering the first and second half. There’s some work to do before this is good enough that you can draw something like a map of Australia from the beginning.
Faster Bezier curves
Most of the rendering time is spent computing points along the Bezier curves. For each t the program is doing a lot of work:
for (uint8_t i = 1; i <= N; i++) {
double t = static_cast<double>(i) / N;
Point next = (p[0] * pow(1 - t, 3))
+ (p[1] * 3 * t * pow(1 - t, 2))
+ (p[2] * 3 * pow(t, 2) * (1 - t))
+ (p[3] * pow(t, 3));
// Draw a line from the previous point to next
}
You can be a lot smarter about calculating this. The general Bezier formula from before can be rewritten as:
\[P = f(t) = K_0 + K_1t + K_2t^2 + K_3t^3\]where
\[K_0 = P_0\] \[K_1 = 3(P_1-P_0)\] \[K_2 = 3(P_2 - 2P_1 + P_0)\] \[K_3=P_3 - 3P_2 + 3P_1 - P_0\]The four Ks can be calculated just once at the beginning and then used to calculate the points along the curve in a slightly simpler way than the original formula. But there is still a lot of work going on. The thing to notice is that what we’re doing here is calculating successive values of a polynomial at fixed intervals. I happened to write a post about that problem a few months ago because that’s exactly what the difference engine was made to solve. The difference engine used divided differences to solve that problem, and we can do exactly the same.
To give a short recap of how divided differences works, if you want to calculate successive values of a n-degree polynomial, let’s take the square function, you can do it by calculating the first n+1 values,
\[\begin{array}{l} 0 \\ \\ 1 \\ \\ 4 \end{array}\]calculate the distances between those values (the first differences) and then the distances between those (the second difference),
\[\begin{array}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 \end{array}\]You can then calculate successive values of the polynomial using only addition, by adding together the differences:
\[\begin{array}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 \end{array} \quad\to\quad \begin{array}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 & \tiny{+0} \\ 4 && \bf{2} \end{array} \quad\to\quad \begin{array}{l|l|l} 0 \\ & 1 \\ 1 && 2\\ & 3 \\ 4 & \tiny{+2} & 2 \\ & \bf{5} \end{array} \quad\to\quad \begin{array}{l|l|l}0 \\ & 1 \\ 1 && 2 \\ & 3 \\ 4 && 2 \\ \tiny{+5} & 5 \\ \bf{9} \end{array}\]You don’t need the full table either, just the last of each of the differences:
\[\begin{array}{l|l|l}&&2\\&5&\tiny{+0}\\9 &\tiny{+2}&2\\ \tiny{+7}&7\\ \bf{16}\\\end{array} \quad\to\quad \begin{array}{l|l|l}&&2\\&7&\tiny{+0}\\16&\tiny{+2}&2 \\ \tiny{+9}&9\\ \bf{25}\\ \end{array} \quad\to\quad \begin{array}{l|l|l}&&2\\&9&\tiny{+0}\\25&\tiny{+2}&2 \\ \tiny{+11}&11\\ \bf{36}\\ \end{array} \quad\to\quad \dots\]We can do the same with the Bezier, except that it’s order 3 so we need 4 values and 3 orders of differences:
Point d0 = /* The same formula as above for t=0.0 */
Point d1 = /* ... and t=(1.0/N) */
Point d2 = /* ... and t=(2.0/N) */
Point d3 = /* ... and t=(3.0/N) */
// Calculate the differences
d3 = d3 - d2;
d2 = d2 - d1;
d1 = d1 - d0;
d3 = d3 - d2;
d2 = d2 - d1;
d3 = d3 - d2;
// Draw the segments
for (uint8_t i = 1; i <= N; i++) {
d0 = d0 + d1;
d1 = d1 + d2;
d2 = d2 + d3;
Point next = d0;
// Draw a line from the previous point to next
}
For each loop D0 will hold the next point along the curve. That’s not bad. At this point we’re only doing a constant amount of expensive work at the beginning to get the four Di and the rest is simple addition. It would be great through if we could get rid of more of the expensive work, and we can.
Let’s say we want n line segments per curve, and let’s define \(d = \frac 1n\). Then the first four values we need for the differences are:
\[f(0) = K_0\] \[f(d) = K_0+K_1d+K_2d^2+K_3d^3\] \[f(2d) = K_0+2K_1d+4K_2d^2+8K_3d^3\] \[f(3d) = K_0+3K_1d+9K_2d^2+27K_3d^3\]That makes the four differences:
\[D_0 = K_0\] \[D_1 = K_1d + K_2d^2 + K_3d^3\] \[D_2 = 2K_2d^2 + 6K_3d^3\] \[D_3 = 6K_3d^3\]This means that instead of calculating the full values and the subtracting them from each other we can plug in the four points to calculate the Ks and then use them to calculate the Ds. Coding this is straightforward too:
static const double d = 1.0 / N;
// Calculate the four ks.
Point k0 = p[0];
Point k1 = (p[1] - p[0]) * 3;
Point k2 = (p[2] - p[1] * 2 + p[0]) * 3;
Point k3 = p[3] - p[2] * 3 + p[1] * 3 - p[0];
// Calculate the four ds.
Point d0 = k0;
Point d1 = (((k3 * d) + k2) * d + k1) * d;
Point d2 = ((k3 * (3 * d)) + k2) * (2 * d * d);
Point d3 = k3 * (6 * d * d * d);
// ... the rest is exactly the same as above</span>
This makes the initial step somewhat less expensive. But it turns out that we can get rid of the initial computation completely if we’re willing to fix the number of segments per curve at compile time.
Transformations
Even better than calculating the Ki and Di for each curve while running would be if we could calculate the Di ahead of time and store those instead of the Pi. That way we would only need to do the additions, there would be no multiplication at all involved in calculating the line segments. It should be easy – the Ds only depend on n (through d) and the Ps and all those are known at compile time.
Well actually no because it’s not the compile time known Ps that are being used here, it’s the result of multiplying them with the view matrix, which is how navigation is implemented. And that matrix is calculated based on input from the joysticks so it’s as compile time unknown as it could possibly be.
The matrix transformation itself is simple, it produces a \(P' = (x', y')\) from a \(P = (x, y)\) by doing:
\[x' = a_x x + b_x y + c_x\] \[y' = a_y x + b_y y + c_y\]which I’ll write as
\[P' = M \cdot P\]where M is a 3 by 2 matrix. That doesn’t mean that precomputing the Ds is impossible though. If you plug the definition of P’ into the definitions of the Ks and Ds it’s trivial to see that the post-transformation D0, \(D_0'\), is simply
\[D_0' = M \cdot D_0\]It takes a bit more work for the other Ds but it turns out that for all of them it holds that:
\[D_i' = M \times D_i\]Where \(\times\) is the same as \(\cdot\) except that the constant factor is left out. So
\[P' = M \times P\]is defined as
\[x' = a_x x + b_x y\] \[y' = a_y x + b_y y\]So you can precompute the Ds and still navigate the image if you just apply the transformation matrix slightly differently. And calculating the Ds is simple enough that it can be made a compile time constant if the Ps are compile time constant, which they are.
#define K0(P0) (P0)
#define K1(P0, P1) ((P1 - P0) * 3.0)
#define K2(P0, P1, P2) ((P2 - (P1 * 2.0) + P0) * 3.0)
#define K3(P0, P1, P2, P3) (P3 - (P2 * 3.0) + (P1 * 3.0) - P0)
#define D0(P0) K0(P0)
#define D1(P0, P1, P2, P3) ((((K3(P0, P1, P2, P3) / kN) + K2(P0, P1, P2)) / kN + K1(P0, P1)) / N)
#define D2(P0, P1, P2, P3) ((((3.0 * K3(P0, P1, P2, P3) / N) + K2(P0, P1, P2)) * 2.0) / (N * N))
#define D3(P0, P1, P2, P3) (6.0 * K3(P0, P1, P2, P3) / (N * N * N))
With this change the curve drawing routine becomes trivial:
// Read the precomputed ds into local variables
Point d0 = d[0];
Point d1 = d[1];
Point d2 = d[2];
Point d3 = d[3];
// Draw the segments
for (uint8_t i = 1; i <= N; i++) {
d0 = d0 + d1;
d1 = d1 + d2;
d2 = d2 + d3;
Point next = d0;
// Draw a line from the previous point to next
}
If you compare this with the initial implementation this looks very tight, it’s hard to imagine how you can improve upon drawing parametric curves using only addition. But there is one place.
The thing is, all these additions are done on floating-point numbers and the Arduino only has software support for floating-point, not native. So even if it’s only addition it’s still relatively expensive. The last step will be to change this to using pure integers.
Fixed point numbers
The display I’m drawing this on is quite small so the the numbers that are involved are quite small too. A 32-bit float gives much more precision than we need. Instead we’ll switch to using fixed-point numbers. It’s pretty straightforward actually. Any floating-point value in the input you multiply by a large constant, in this case I’ll use 216, and then rounded the result to a 32-bit integer. Then you do all the arithmetic on that integer, replacing floating-point addition, multiplication and division by constants, etc., with the corresponding integer operations. Finally just before rendering any coordinates on the display you divide by the constant, this time by left-shifting by 16, and the result will be very close to the same as you’d have gotten using floating point. You can get it close enough that the difference isn’t visible. And even though the Arduino doesn’t have native support for 32-bit integers either they’re still a lot faster than floats.
Multiplying by 216 means that we can represent values between -32768 and 32767, with a fixed accuracy of around 10-5. That turns out to be plenty of range for any number we need for this size display even at the max zoom level but the accuracy is slightly too low as you can see in this video:
When going from floating to fixed point directly you end up with these visible artifacts. There is a relatively simple fix for that though. The problem is caused by these two, the precomputed values of D2 and D3:
#define D2(P0, P1, P2, P3) ((((3.0 * K3(P0, P1, P2, P3) / N) + K2(P0, P1, P2)) * 2.0) / (N * N))
#define D3(P0, P1, P2, P3) (6.0 * K3(P0, P1, P2, P3) / (N * N * N))
In both cases we’re calculating a value and then dividing it by a large number, the number of segments per curve squared and cubed respectively. Later on, especially when you zoom in, you’re multiplying them with a large number which magnifies the inaccuracy enough that it becomes visible. The solution is to not divide by those constants until after the matrix transformation. That makes the artifacts go away. It’s a little more work at runtime but at the point where we’re doing it we’re working with integers so if N is a power of 2 the division is actually a shift.
At this point the slowest part is shipping the data to the LCD. It turns out there were some opportunities to improve that as well so the very last step is to do that.
Faster serial
The data connection to the display is serial so every single bit goes over just a single pin using SPI. The Arduino has hardware support for SPI on a few pins so that’s what I’m using. The way you use the hardware support from C code is like this (where c is a uint8_t):
SPDR = c;
while (!(SPSR & (1 << SPIF)))
;
You store the byte you want to send at a particular address and then wait for the signal that the transfer is done by waiting for a particular bit to be set at a different address. We’re doing this for each byte so that’s a lot of busy waiting for that bit to flip. The first improvement is to flip them around,
while (!(SPSR & (1 << SPIF)))
;
SPDR = c;
Now instead of waiting before continuing we continue on immediately after starting the write, and then we wait for the previous SPI write to complete before starting the next one. If there is any work to be done between sending two pixels, and it does take a little work to decode the buffer and decide what to write out, we’re now doing that work first before waiting for the bit to flip.
Also, a great way to make sending data fast is to send less data. By default you send 18 bits per pixel but the display allows you to send only 12. In 12 bit mode you send two pixels together in 3 bytes. You switch to 12 bit mode by changing the init sequence slightly.
Patching these two changes into the underlying graphics library shaves around 25% off the time to flush to the display. It also means that you can’t just load my code and run it against the vanilla libraries but the tweaks you need are absolutely minimal.
The results
That’s it, you’ve seen every single trick I used. Here’s a longer video that shows different segment counts, from quite coarse with a decent frame rate to very smooth but somewhat slow.
When I say “decent frame rate” I don’t mean “Peter Jackson thinks this looks good”. What I mean is that the display is refreshed often enough that when you move the joysticks you get feedback quickly enough that you can actually navigate without getting lost. If it takes 500ms to refresh it becomes almost impossible, or at least really frustrating, to zoom in on a detail; if it takes 150ms it’s not a problem. And with the final version you can do that even at 32 segments per curve. It’s not super pretty but fast enough that using the navigation is not a problem.
If you were so inclined you could squeeze this even more especially if you get a parallel rather than a serial connection to the display to get the flush delay down. The reason I’m actually playing around with Bezier curves is for a different project with different components and those remaining improvements won’t help me for that. But with a parallel connection I do suspect you can get the frame rate as high as 20 FPS with this setup. I’ll leave that to someone else though.