Monthly Archives: August 2014

Z-Quads: Containment

Posted on August 26, 2014 | 3 Comments

This is the second post about z-quads, a spatial coordinate system. In the first post I outlined how they work and described how to jump between quads at different zoom levels. In this post I’ll look at how to determine whether one quad contains another, and how to find the common ancestor of two quads.

Containment

Given two quads q and s, how do we determine if q contains s? It’s pretty simple – there’s two cases to consider.

The one case is that the zoom level of q is higher than the zoom level of s. (Let’s call them z_q and z_s). If q is zoomed in more than s then it can’t contain s because it’s clearly smaller. So now let’s assume that q is at the same level or higher than s. If s is contained in q then that’s just another way of saying that q is s‘s ancestor. So if you get the ancestor of s that’s at the same level as q then you should get – q. In other words,

contains?(q, s) = (z_q ≤ z_s) and (ancestor(s, z_s – z_q) = q)

Pretty simple right? By the way, now you’re seeing why I pointed out before that the ancestor operation is defined for n=0: that’s what you’re using if you do contains?(q, q), which obviously you’d expect to be true.

This is the first operation where the zoom level appears explicitly and I’ll get into how to determine that for a given quad in a second. But first I’ll complete containment and talk about finding the most specific common ancestor of two quads.

Common ancestor

Let’s say we have two quads, call them q and s again, and you want to find the most specific ancestor of the two. That is, the ancestor that contains both of them and where no child also contain them both – since that would make the child more specific. This is well-defined since any two quads have, if no other, at least the trivial ancestor 0 in common.

The first step is to normalize q and s to the same zoom level. We’ll assume that s is zoomed in at least as much as q – if it’s not you can always just have an initial step that swaps them around. We can zoom s out to z_q and it won’t change what their common ancestor is because we know that is has to be at level z_q or above for it to be an ancestor of q. Let’s use t to refer to the result of zooming s out to q‘s level. So now we have q and t which are both a zoom level z_q.

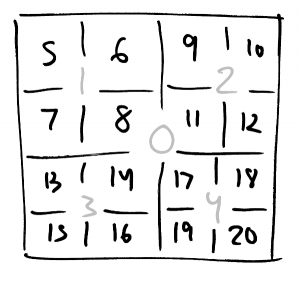
To do the rest of the computation we need a bit more intuition about how the space of quad scalars is structured. As I’ve mentioned a few times at this point, because quads are numbered in z-order within one level all the descendants of a particular quad are contiguous, and so are the scalars. That means that you can split the binary representation of a scalar into 2-bit groups where each group corresponds to a subdivision of the whole space.

Here’s an illustration of how that works out for the scalars at zoom-2. You can think of the binary representation of the scalar, here for instance 9, as consisting of two groups: the top two bits indicate which 2×2 subdivision the quad belongs to, and the bottom two bits as the 1×1 subsubdivision within that one.

If you’re given two scalars, let’s take 9 and 11, and you write their binary representations together, then their common ancestor almost jumps out at you,

 9: 10 01
11: 10 11

You can tell from the top two bits that they’re both in the same subdivision but then they’re in different subsubdivisions. So the most specific common ancestor is the one that’s filled with 8s above.

This gives you a hint of how to find the most specific common ancestor more generally: you take the two scalars, then you see which 2-bit groups are different, and then you zoom out just enough that you discard all the groups that are different and keep the ones that are the same. You can find the highest bit where two numbers are different by xor’ing them together and taking the highest 1-bit in the result:

   9: 10 01
  11: 10 11
 xor: 00 10

Here the highest different bit is at 2 so they’re different at the lowest zoom level but then they’re the same. So their most specific common ancestor is the quad you get by zooming out one step from either of them. More generally, the formula for getting the most specific common ancestor of two quads q and t at the same zoom level z is,

msca(q, t, z) = ancestor(q, ffs((q – b_z xor t – b_z) + 1) / 2)

Here ffs is find-first-set which returns the index of the highest 1-bit in a word, 0 if there are none. The (x+1)/2 part is to get from a bit index to a zoom level. For instance if the highest set bit is 1 or 2, as in the example, (x+1)/2 will be 1.

At this point let’s just recap quickly. Given a quad you can get an ancestor, a descendant, and you can determine how it is related to any of its ancestors. Given two quads you can determine whether one contains the other, and you can find the most specific common ancestor. All in a constant, low, number of bit operations. There are more operations to come but already I think we’ve got a big enough library of operations to be useful.

I’ve glossed over a few things along the way though, particularly how to determine the zoom level for a given quad. That’s what I’ll talk about next. It’s kind of fiddly so if you’re okay with trusting that it can be calculated efficiently then you can just skip this part and go on to the part where I talk about how to convert from regular floating point coordinates to quads and back.

Otherwise, let’s go.

Zoom

Given a quad, what is its zoom level?

Since quads at higher zoom levels have higher numeric values one way to answer this is to just compare with the biases. If a value is between b₄ and b₅ then it must have zoom level 4, and so on. Since the biases are sorted you can even do binary search. But you can be a lot smarter than that.

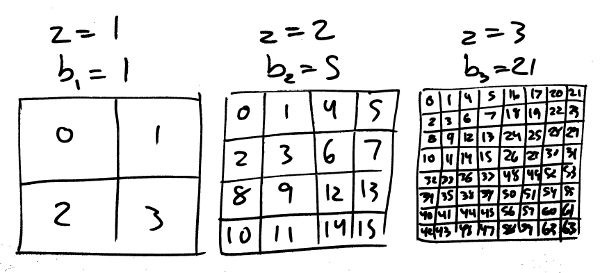
Here’s an illustration of where the quads at zoom level 4 and 5 are located on the numbers line,

The zoom-4 quads start at 85 and end at 340, then the zoom-5 quads start at 341 and run until 1364 where zoom-6 starts. Each range of quads contains values from three different 2-power intervals: zoom-4 contains values from the 2⁶ to the 2⁸ interval, zoom-5 from 2⁸ to 2¹⁰, and so on. This suggests that determining the highest set one-bit in the quad is a good place to start.

As an example, say the highest one-bit is 8 or 9. That is, the quad is between 256 and 1024. If you look at the numbers line then you see that there are two possibilities: if it’s smaller than b₅, 341, then it’s at level 4, otherwise it must be at level 5. Similarly, if the highest bit is at index 10 or 11, that is a value between 1024 and 4096, then the level is 5 or 6 depending on whether the quad is larger than b₆, 1365.

There’s a general principle working here. Say highest set bit of a quad is at index k. The zoom level will be c=k/2 if the quad is is smaller than b_c+1, otherwise it’s c+1.

As an illustration, let’s try this with one of the quads from the introduction, 171171340006. The highest 1-bit is at index 37 so c is 18. This means that that quad is at zoom level 18 or 19. The boundary between the two is b₁₉ which is 91625968981. This is less than the quad’s value so the result must be 19.

Okay so this almost gives us a fast way to calculate the zoom level. The one thing that’s missing is: how to get an arbitrary zoom bias quickly – how do you know that b₁₉ is 91625968981? There’s only a small number of bias values of course so you can just put them in a table, but you can also calculate them directly. The thing to notice is that the binary representation of a bias is simple:

b₃: 10101 (= 21)     
b₄: 1010101 (= 85)   
b₅: 101010101 (= 341)

…and so on. They’re all alternating ones and zeroes. That’s because, as we saw before, they are made up of sums of powers of 4. That gives us a practical way to calculate them: take the binary number that consists of alternating 0s and 1s and mask out the bottom part of the appropriate size. So for b₃ we mask out the bottom 5 bits, for b₄ the bottom 7 and so on:

b_z = 0x5555555555555555 & ((1 << 2 z) - 1)

I imagine there might be more efficient ways but this one works.

Calculating the zoom level isn’t particularly expensive but you need it for most operations so in my own code I typically compute it once early on and then keep it cached along with the quad itself (though it’s not something you would ever store or transmit along with the quad since it’s redundant). Even for some of the operations where you technically don’t need it it’s still useful to have it. For instance, you can get nth ancestor of a quad without knowing the zoom, but the operation is only well-defined if the quad’s zoom is n or greater so it’s nice to have the zoom around so you can make that assertion explicitly in the code.

I think that’s enough for one post. In the next part we’ll talk about how to do conversion between coordinates and quads.

→ 3 Comments

Posted in z-quads

Z-Quads: Construction

Posted on August 25, 2014 | 10 Comments

This post is about a spatial coordinate system I’ve been playing around with, z-quads. Unlike most commonly used coordinate systems a z-quad doesn’t represent a point but a square with an area.

To the right are some examples of quads of increasing accuracy, gradually zooming in on Århus. (The quads are the red rectangles). The first one that covers northern Germany, some of England, and half of Denmark, is quad 637 which has zoom level 5. The one that covers all of Århus is 163241 which has zoom level 9. Going further down to zoom level 15 is 668638046 which covers part of the center of Århus, and finally at zoom level 19 is 171171340006 which covers just a couple of houses.

This should give a rough sense of how the system works. A quad is an integer, typically 64 bits, which represents some square area on the earth. Each quad has a zoom level associated with it and higher numbers have higher zoom levels. There’s a lot more to it than that but that’s the core of it.

Below I’ll describe how z-quads are constructed, which is pretty straightforward. Then I’ll look at how to operate on them: how to convert to and from them, zoom in and out, that kind of thing.

Divide, divide, divide some more

For a hobby project I’m working on I needed to represent a large set of geographic coordinates. They happen to represent positions of bus and train stops but that’s not super important. To the right is a diagram that illustrates what I had in mind when I started playing around with this. What I wanted really was a way to divide the world evenly into squares of different sizes that I could divide my positions into. (For simplicity I’ve scaled the world down to a 1×1 unit square). Each of the three colored squares here should have some unique integer id. When I say “divide the world evenly” I mean that they’re not arbitrary squares, they’re on the grid you get if you divide the whole square into in four equal parts, then divide each of those into four as well, and so on and so on.

It seemed intuitively reasonable that you’d want the entire space to be represented by 0.

This is zoom level 0. Zooming down one level, you might divide 0 into four parts and call them 1-4,

This is zoom level 1. Then you can keep going and do the same again to get zoom level 2,

At each new zoom level you add 4 times as many new quads as you had on the previous level so where level 2 has 16, level 3 will have 64 and level 4 will have 256.

This is how z-quads are constructed. Pretty simple right? Already, by the way, we know the id of the blue square from the beginning because it’s there at zoom level 2: it’s quad 14. And just as a reminder, at this point we’re playing around on the unit square but it’s just a matter of scaling the values back up to get coordinates on the earth. Here’s 14 again, scaled back up:

One thing you may notice if you look closely at how the quads at zoom level 2 are numbered is that they look of out of sequence. You might expect them to be numbered 5-8 on the top row, 9-12 on the next, and so on. Instead they’re numbered in zig-zag, like this:

So they zig-zag within each of the four parts of the big square, and also when going between the four parts. That’s because it turns out to be really convenient when you divide a quad to have all the quads in the subdivisions be contiguous. So the children of 1 are 5-8, of 2 are 9-12, and so on. We’ll end up relying on that constantly later on. (The numbering within each level it known as a Z-order or Moreton order curve).

Okay, so now I’ve postulated way to divide the unit square, by which I mean the surface of the earth, into regular parts. The next step is to figure out how to operate on them which is where it’ll become clear why this number is is particularly appealing.

Zoom bias

Given a quad there are many operations that you might conceivably want to perform. You might want to know which quad is its parent (that is, the quad that contains it at the zoom level above) or the parent’s parent, etc. Given two quads you might want to know whether one contains the other. Or you might want to find the most specific quad that contains both of them.

The first thing we’ll look at is how to get the parent of a quad. To explain that I need to introduce two contepts, zoom bias and a quad’s scalar. The zoom levels we’ve seen so far (and a few more) and the values of their quads are

Zoom 0: 0
Zoom 1: 1-4
Zoom 2: 5-20
Zoom 3: 21-84
Zoom 4: 85-341

In general, at level z you have 4^z quads, so at level 2 you have 4²=16, the first one being 5. At level 3 you have 4³=64, the first one being 21, and so on.

The value of the first quad for a given zoom level turns out to appear again and again when doing operations so I’ll give that a name: the zoom bias. When I talk about the zoom-3 bias, which I’ll typically write as b₃, what I’m referring to is 21 since that is the value of the first quad at zoom level 3.

The scalar of a quad is its value minus the bias of its zoom level. Here are the biases and scalars for zoom levels 1 to 3:

Parents and children

Now we’re ready to look at how you get a quad’s parent. As mentioned, quads are numbered such that the subquads of each parent are contiguous. That obviously also holds for the scalars. That means that if you divide the scalar value by 4, the number of children in each parent, this happens:

You get the scalar of the parent. So given a quad q at zoom level z, the parent quad can be computed as

parent(q) = ((q – b_z) / 4) + b_z_-1

Unbias the quad to get the scalar, divide it by 4 to get the parent’s scalar, then add the parent’s zoom level bias to get back a quad. And in fact this can be simplified if you use the fact that the zoom biases are related like this,

b_z+1 = 4b_z + 1

I’ll justify this in a moment but for now you can just take it as a given. If you plug this in and simplify you get that

parent(q) = (q – 1) / 4

(By the way, except when stated explicitly all values are integers so division implicitly rounds down). What’s neat about the simplified version is that b_z no longer appears so you can apply this without explicitly knowing the zoom level. It’s pretty easy to calculate the zoom level for a quad, I’ll go over that in a bit, but it’s even easier if you don’t have to.

How about going the other way? Given a quad, finding the value of one of its children? That’s the same procedure just going the other way: unbias the parent, multiply by 4, add the child’s index (a value from 0 to 3), rebias:

child(q, i) = 4(q – b_z) + i + b_z₊₁

Again this can be simplified by using the relation between the zoom biases to

child(q, i) = 4q + i + 1

If instead of the child’s index (from 0 to 3) you use its quad value (from 1 to 4) it becomes even simpler,

child(q, i) = 4q + i

This is part of why they’re called z-quads: it’s from all the z-words. The numbering zig-zags and it’s easy to zoom in and out, that is, get between a quad and its parent and children. (If, by the way, you’ve ever used a d-ary heap you may have noticed that this is the same operation used to get the child node in a 4-ary heap).

Since you can calculate the value of a child quad given its parent it also means that you can calculate the value of a quad one zoom level at a time, starting from 0. For instance, in the original example with the colored squares the blue square was child 2 of child 3 of 0. That means the value is

child(child(0, 3), 2) = 4 (4 0 + 3) + 2 = 4 3 + 2 = 12 + 2 = 14

Which we already knew from before of course. This isn’t how you would typically convert between positions and quads in a program, there’s a smarter way to do that, but I’ve found it useful for pen-and-paper calculations.

Ancestors and descendants

Now we know how to go between a quad and its parent and children we can generalize it to going several steps. When going multiple steps, instead of talking about parents and children we’ll talk about ancestors and descendants. An ancestor of a quad is its parent or one of the parent’s ancestors. A descendant of a quad is one of its children or one of the children’s descendants.

It turns out that just as there’s a simple formula for getting a quad’s parent there is one for getting any of its ancestors:

ancestor(q, n) = (q – b_n) / 4ⁿ

Given a quad this gives you the ancestor n steps above it. The special case where n is 1 is the parent function from before, b₁ being 1. Even though it might not seem sensible now it’s worth noting for later that this is also well-defined for n=0 where the result is q. So a quad is its own 0th ancestor.

It’s easy to prove that the ancestor function is correct inductively by using a second relation that holds between the b_zs:

b_z₊₁ = 4^z + b_z

I won’t do the proof here but maybe we should take a short break and talk about why these relations between the biases hold. The bias at a zoom level is the index of the first quad at that level. At level 0 there is 1 (=4⁰) quad so b₁, the next available index, is 1. At level 1 there are 4 (= 4¹) which start from 1 so the next bias is

b₂ = 4⁰ + 4¹ = b₁ + 4¹ = 5

If we keep going, the next level adds 16 (= 42) quads in addition to the 5 we already have which makes the next bias

b₃ = 4⁰ + 4¹ + 4² = b₂ + 4² = 21

You can see how each bias is a sum of successive powers of 4 which gives you the relation I just mentioned above, that to get the next bias you just add the next power of 4 to the previous bias.

b₃ = b₂ + 4²

It also gives us the other relation from earlier,

b₃ = 4⁰ + 4¹ + 4² = 4⁰ + 4(4⁰ + 4¹) = 4 b₂ + 1

Okay so back to ancestors and descendants. As with ancestors you can also get to arbitrarily deep descendants in one step,

descendant(q, c, n) = 4ⁿ q + c

This gives you the descendant of q which relates to q the same way quad c, which has zoom level n, relates to the entire space. This can again be proven by induction with the base case being the child operation from before. And again this is well-defined for n=0 where the result is q.

So now we can jump directly between a quad and the quads related to it at zoom levels above and below it. This will be the building blocks for many other operations. But before we go on to the next part I’ll round off the ancestor/descendant relation with the concept of descendancy.

When you go from a quad to one of its ancestors you’re in some sense discarding information. If you start with a quad that covers the center of Århus from the initial example and zoom out to the one covering northern Europe, you’ve lost the information about where specifically in northern Europe you were. You can add that information back by using the descendant operation, but for that you need to know c, the quad that describes where within northern Europe the Århus quad is. That is, you need to know the descendancy of the Århus quad within the northern Europe quad. There is a simple way to calculate the descendancy of a quad within the ancestor n steps above it,

descendancy(q, n) = ((q – b_n) mod 4ⁿ) + b_n

The descendancy is a little less intuitive than the others, that’s also why I’m not spending more time on how it’s derived or proving it correct, but it turns out that it’s actually quite useful when you work with quads in practice. And it definitely feels like the model would be incomplete without it. Note again, as always, this is well-defined when n=0 where it yields 0 (as in, any quad spans the entirety of itself).

Now we have a nice connection between the three operations: for all q and n where the operations are well-defined it holds that,

q = descendant(ancestor(q, n), descendancy(q, n), n)

With these basic building blocks in place we’re ready to go on to some higher-level operations, the first ones will be the two containment operations. Given quads q and s, is s contained in q? And given two quads, determine the most specific ancestor that contains both of them. For those you’ll have to go on to the next post, z-quads: containment.

(Update: hacker news discussion)

(Update: added some references mentioned in the discussion: z-order, d-ary heaps. Remove part where I couldn’t find other non-point coordinate systems)

→ 10 Comments

Posted in Uncategorized